Lección práctica número 9 derivada del tema. Lección práctica "cálculo de derivados"
Trabajo practico
matemáticas
1. Encontrar el límite de una función. El primero y el segundo son límites maravillosos.
2. Derivada de una función compleja. Estudio de una función de una variable y trazado de gráficas.
3. Prueba “Aplicación del cálculo diferencial al estudio de funciones”.
4. Encontrar integrales indefinidas. Cálculo de integrales definidas.
5. Cálculo de determinantes.
6. Resolución de sistemas de ecuaciones lineales mediante el método de Cramer. Prueba.
7. Resolución de problemas sobre el tema “Conjuntos”. Fórmulas de álgebra lógica.
8. Cálculo de probabilidades de eventos aleatorios. Fórmula de probabilidad total.
9. Cálculo de características numéricas.
10. Prueba “Fundamentos de la teoría de la probabilidad y la estadística matemática”
11. Forma trigonométrica de un número complejo.
12. Acciones con números complejos en diversas formas.
INSTRUCCIONES METODOLÓGICAS PARA EL TRABAJO PRÁCTICO EN MATEMÁTICAS
CURSO 2
Una lección práctica es una forma de organización del proceso educativo, que implica que los estudiantes realicen uno o más trabajos prácticos por encargo y bajo la dirección de un profesor.
Así, en las clases prácticas de matemáticas, los estudiantes desarrollan la capacidad de resolución de problemas, que en el futuro deberían utilizarse para resolver problemas profesionales en disciplinas especiales.
En el curso del trabajo práctico, los estudiantes dominan la capacidad de utilizar fuentes de información, trabajar con documentos reglamentarios y materiales educativos, libros de referencia, realizar dibujos, diagramas, tablas, resolver diversos tipos de problemas y realizar cálculos.
Problemas que se resuelven durante las lecciones prácticas de matemáticas:
1) ampliación y consolidación de los conocimientos teóricos en matemáticas adquiridos durante las clases magistrales;
2) desarrollar en los estudiantes las habilidades y destrezas prácticas necesarias para resolver con éxito problemas en matemáticas;
3) desarrollo de la necesidad de autoeducación de los estudiantes y mejora de conocimientos y habilidades en el proceso de estudio de las matemáticas;
4) formación de una actitud creativa y un enfoque de investigación en el proceso de estudio de las matemáticas;
5) formación de cualidades profesionalmente significativas de un futuro especialista y habilidades para aplicar los conocimientos adquiridos en el campo profesional.
Lección práctica nº 1. Cálculo de límites de funciones. El primero y el segundo son límites maravillosos.
Sujeto : Cálculo de límites de funciones.
Objetivo: Adquisición de conocimientos básicos en el campo de las ramas fundamentales de las matemáticas. . Probar la asimilación de conocimientos sobre el cálculo de los límites de funciones. Repetir y sistematizar conocimientos sobre este tema.
Tareas:
Desarrollo del pensamiento profesional creativo;
Dominio del lenguaje científico, habilidades para operar conceptos;
Dominar las habilidades para plantear y resolver problemas;
Profundizar la formación teórica y práctica;
Desarrollo de la iniciativa y la independencia de los estudiantes.
Fortalecimiento de las habilidades informáticas;
Continúe trabajando en el habla matemática.
Formación de habilidades para el trabajo independiente, trabajo con un libro de texto, habilidades para la adquisición de conocimientos de forma independiente;
Desarrollo de la capacidad de resaltar lo principal al trabajar con texto;
Formación del pensamiento independiente, operaciones mentales: comparación, análisis, síntesis, generalización, analogía;
Mostrar a los estudiantes el papel del trabajo sistemático en la profundización y fortalecimiento de los conocimientos, en la cultura de realización de tareas;
Desarrollo de las habilidades creativas de los estudiantes.
Proporcionar trabajo práctico:
Material teórico de recomendaciones metodológicas para trabajos prácticos.
Matemáticas, – Serie: Educación secundaria profesional. - Rostov del Don “Phoenix”, pág.
Progreso de la lección práctica.
1.Formulación del tema de la lección, explicación de la conexión del tema con otros temas de la disciplina académica;
2.Verificar la preparación de los estudiantes para la clase;
3. Realización de la lección propiamente dicha según el tema y de acuerdo con el programa de trabajo de la disciplina:
Estudiar material teórico sobre el tema "Cálculo de los límites de funciones".
Considere ejemplos de resolución de tareas típicas.
Realice un trabajo independiente para calcular los límites de funciones utilizando el primer y segundo límites notables.
Responder preguntas de seguridad.
Información teórica y recomendaciones metodológicas.
sobre la resolución de problemas.
1. Presentación de material teórico.
Para calcular el límite de una función en un punto, necesitas:
1) Sustituir en lugar de la variable x lo que tiende x.
2) Si después de completar el paso 1) obtenemos una incertidumbre del formulario https://pandia.ru/text/78/405/images/image003_6.png" width="19" height="22 src=">y reemplazar la flecha con un menos: (x-a).
3) Si, después de completar el paso 1), recibimos una incertidumbre del formato https://pandia.ru/text/78/405/images/image002_13.png" width="18" height="31 src="> Asociado a los valores de funciones trigonométricas, debemos utilizar el primer límite destacable.
Definición. El primer límite notable se llama límite.
https://pandia.ru/text/78/405/images/image007_4.png" alt="$\displaystyle \lim_(x\to0)\dfrac(\sin x)(x)=1. $" width="102" height="52">!}
5) Definición:El segundo límite destacable llamado límite

El número dado por este límite juega un papel muy importante tanto en el análisis matemático como en otras ramas de las matemáticas. el numero se llama base de logaritmos naturales ( https://pandia.ru/text/78/405/images/image009_4.png" alt="$ e$" width="11" height="14">показывает, что -- иррациональное число, несколько первых десятичных знаков которого таковы:!}
![]()
2. Consolidación del material estudiado.
Ejemplo 1
https://pandia.ru/text/78/405/images/image015_1.png" width="28" height="30 src=">= -4
Usamos la regla 1) y sustituimos en lugar de x lo que x debería esforzarse, es decir, x=2.
Ejemplo 2
https://pandia.ru/text/78/405/images/image017_1.png" ancho="154" alto="32 src=">.png" ancho="21" alto="30 src=">= 5
Ejemplo 3
https://pandia.ru/text/78/405/images/image021_1.png" width="199" height="37 src=">.png" width="137" height="35 src=">. png" ancho="138" alto="24 src=">=3+3=6
Ejemplo 4
https://pandia.ru/text/78/405/images/image004_7.png" width="22" height="31 src=">.png" width="104" height="46 src=">. png" altura="30 src=">
Ejemplo 5
https://pandia.ru/text/78/405/images/image032_0.png" width="61" height="46 src=">.png" height="30 src=">=2
Ejemplo 6
https://pandia.ru/text/78/405/images/image036_0.png" width="18" height="28 src=">
b) 
V) 
3. Consolidación de conocimientos, habilidades y habilidades.
Realizar un trabajo independiente para calcular los límites de funciones.
Trabajo práctico nº 1. Opción 1 Calcula el límite de la función: 1. 2. 3. 10. | Trabajo práctico nº 1. opcion 2 Calcula el límite de la función: 1. 2. 3. 10. |
Trabajo práctico nº 2.
Sujeto : Encontrar la derivada de una función. Estudio de una función de una variable y trazado de una gráfica.
Objetivo : Pruebe en la práctica el conocimiento del concepto de derivada de una función, la capacidad de encontrar derivadas de funciones elementales, funciones complejas, funciones inversas, utilizando la tabla de derivadas y reglas de diferenciación, el concepto de función compleja e inversa, la capacidad. utilizar una derivada para estudiar funciones.
Proporcionar trabajo práctico.:
Libro de texto. "Matemáticas". – M.: Avutarda, 2010.
Matemáticas. M: Foro-Infa 2008.
Tarjetas individuales con una práctica opción de trabajo.
1. Material teórico y ejemplos de cómo encontrar la derivada de una función.
Definición: La derivada de la función f(x) (f"(x)) en el punto x es el límite de la relación entre el incremento de la función y el incremento del argumento cuando el incremento del argumento tiende a cero:
https://pandia.ru/text/78/405/images/image061_0.png" ancho="209 altura=235" altura="235">
Reglas de diferenciación.
Si las funciones f(x) y g(x) tienen derivadas, entonces
2. (u+v)′=u′+v′
3. (uv)′=u′v+v′u
4. (C u)′=C u′, donde C=const
5..png" ancho="49" alto="54 src=">
6. Derivada de una función compleja:
f′(g(x))=f′(g) g′(x)
2. Ejemplos.
1..png" ancho="61" alto="41 src=">.png" ancho="20" alto="41 src=">.png" ancho="20" alto="41 src="> .png" ancho="69" alto="41 src=">+4).
La función es el producto de dos factores: u=https://pandia.ru/text/78/405/images/image071_0.png" width="72" height="41 src=">.png" width=" 64" altura="41 src=">.png" ancho="19" altura="41 src=">.png" ancho="45" altura="51 src=">.
La función es el cociente de dos expresiones: u=https://pandia.ru/text/78/405/images/image079.png" width="52" height="41 src=">..png" width= "215" " altura="57 src=">.png" ancho="197 altura=36" altura="36">
Solución. Encontremos la derivada de esta función usando la regla de derivación de funciones complejas (fórmula 6):

5. Si, entonces 
6. y = X 3 – 3X 2 + 5X+ 2. Busquemos y "(–1).
y " = 3X 2 – 6X+ 5. Por lo tanto, y "(–1) = 14.
7. Si y= iniciar sesión X porque X, Eso y" = (en X)" porque X+en X(porque X) " =1/X∙cos X–en X pecado X.
Sea dada una función. Para estudiarlo necesitas:
1) Encuentra su dominio de definición. Si no es demasiado difícil, también resulta útil encontrar el rango. (Sin embargo, en muchos casos, la cuestión de la búsqueda se pospone hasta que se encuentren los extremos de la función).
2) Descubra las propiedades generales de la función que ayudarán a determinar su comportamiento: si la función es par o impar, si es periódica.
3) Descubra cómo se comporta la función cuando el argumento se acerca a los puntos límite del dominio de definición, si existen tales puntos límite. Si una función tiene puntos de discontinuidad, entonces estos puntos también deben verificarse para detectar la presencia de asíntotas verticales de la función. Encuentra asíntotas oblicuas.
4) Encontrar los puntos de intersección de la gráfica con los ejes coordenados, que consiste en simplemente calcular el valor de la función bajo la condición:
Con eje OX: y=0;
Con eje OY: x=0.
Encontrar los puntos de intersección con el eje puede llevar a la necesidad de resolver una ecuación algebraica compleja, lo que, quizás, sólo pueda hacerse de forma aproximada. Habiendo encontrado las raíces de la función y los puntos de discontinuidad, podemos determinar el signo de la función en cada uno de los intervalos entre estos puntos. Esto se puede hacer calculando el valor de la función en cualquier punto del intervalo o utilizando el método del intervalo.
5) Encuentra intervalos de monotonicidad. Para hacer esto, encuentra la derivada y resuelve la desigualdad:
https://pandia.ru/text/78/405/images/image089.png" width="49" height="19 src=">, la función está disminuyendo.
Habiendo encontrado los intervalos de monotonicidad, podemos determinar inmediatamente los puntos del extremo local: donde un aumento es reemplazado por una disminución, se ubican los máximos locales, y donde una disminución es reemplazada por un aumento, se ubican los mínimos locales.
6) Encontrar los intervalos de convexidad y concavidad se realiza utilizando la segunda derivada..png" width="39" height="19 src="> en los intervalos:
si https://pandia.ru/text/78/405/images/image090.png" width="39" height="19 src=">‹0, entonces la curva del gráfico de función es convexa.
Al mismo tiempo, definimos puntos de inflexión como aquellos puntos en los que la función cambia la dirección de la convexidad (y es continua).
7) Encontrar los puntos de intersección de la gráfica con la asíntota y puntos adicionales. Este punto no es obligatorio, pero encontrar dichos puntos hace que el estudio de la función y su gráfica sea completo y completo.
Tenga en cuenta que es útil trazar inmediatamente los puntos en los ejes de coordenadas y en la gráfica que se obtienen durante el estudio de funciones en el dibujo. Esto ayuda a comprender la apariencia del gráfico a lo largo del camino.
3. Hágalo usted mismo:
|
opción | Encuentra la derivada de la función y: |
opción | Encuentra la derivada de la función y: |
1.y=6- | 1.y=-6- 5.y= |
||
1.y=-7-1 | 1.y=-7-1 |
||
1.y=4x-3tgx+6x-8 | 1.y=-5x+2ctgx+3x-2 |
||
lección practica
Sujeto: Encontrar derivadas. Aplicación de la derivada al estudio de funciones y trazado de gráficas.
Objetivo: Domina el cálculo de derivadas, aprende a explorar una función usando la derivada.
Medios de educación: cuadernos para ejercicios prácticos, presentaciones sobre el tema, recursos de Internet.
1. Considere material teórico sobre los temas: “Reglas para calcular derivadas”, “Extremo de una función”, “Convexidad, concavidad. Punto de inflexión."
2. Revisar muestras de tareas.
3. Complete la tarea de prueba número 1.
Preguntas de control:
1. Definir el máximo (mínimo) de una función en un punto. ¿Qué se puede decir sobre el signo del incremento de la función en una vecindad bastante pequeña del punto máximo (mínimo)?
2. ¿Cuáles son las condiciones necesarias para la existencia de un extremo de una función? ¿Cuál es su significado geométrico?
3. ¿Cuál es la regla para encontrar los valores mayor y menor de una función en un segmento?
4. Defina la convexidad (concavidad) de una curva en un intervalo.
5. ¿Cuál es la regla para encontrar los intervalos de convexidad y concavidad de una curva?
6. Punto de inflexión de la curva. ¿Cómo encontrarla?
7. ¿Cuál es el algoritmo para construir la gráfica de una función?
Reglas para calcular derivados.
Derivada de una función compleja.
Si en=ƒ( Y), tu=φ(x), entonces en¢ ( X)=ƒ¢ (i)·φ¢ (X).
Derivada de una suma.
Si en(X)=Y(X)+v (X), Eso en¢ (X)=Y¢ (X)+v ¢ (X)
Derivado del producto.
Si y(x)=u(X)· v (X), Eso en¢ = Y¢ · v + tu · v ¢ .
En particular, ( Con· Y)¢ =c· Y¢, es decir, el factor constante se quita de debajo del signo de la derivada. Es fácil comprobar que
(tu 2 ) ¢ = 2 u·u ¢ , (tú 3 ) ¢ =3u 2 tu ¢ , … , (tú norte ) ¢ =n·u n-1 tu ¢ .
Derivada del cociente.
Si entonces  .
.
tabla de derivados
1. (Con)¢ =0
Para una función compleja: si u=u(x), Eso:
2. (X)¢ =1
3. (X α )¢ = α · Xα–1, A– cualquier número real.
 .
.
3. 

4. (A X ) ¢ =un X · en A
4. 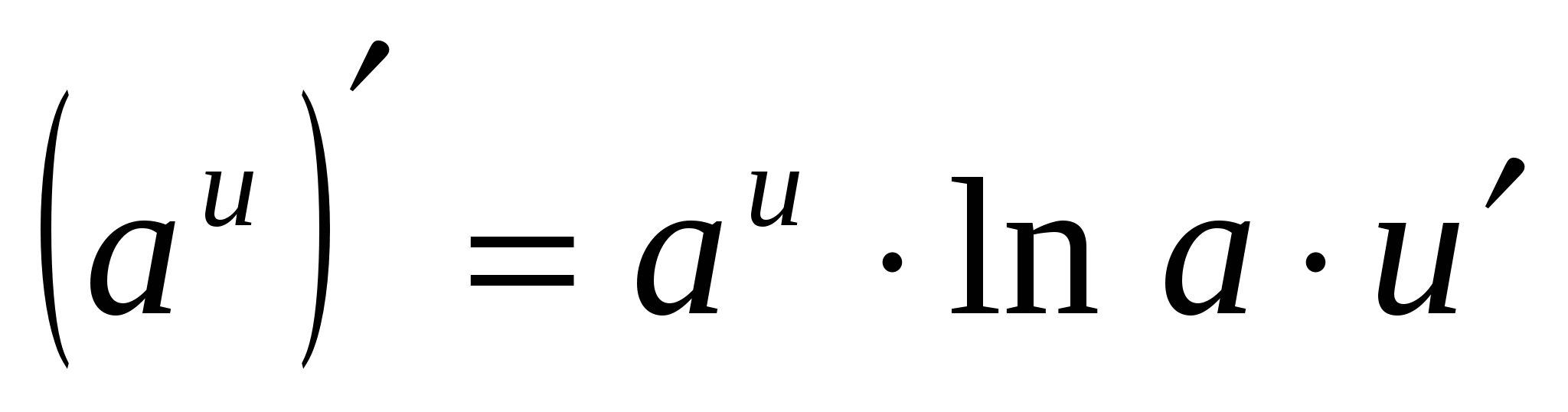

5. (registro
a
X)
¢
=
 .
.
5. 

6. (pecado x)¢ =cos x
6. 
7. (cos x)¢ = –pecado x
7. 
8. (tgx)¢
=
8. 
9. (cuadro x)¢
=
9. 
10. 
10. 
11. 
11. 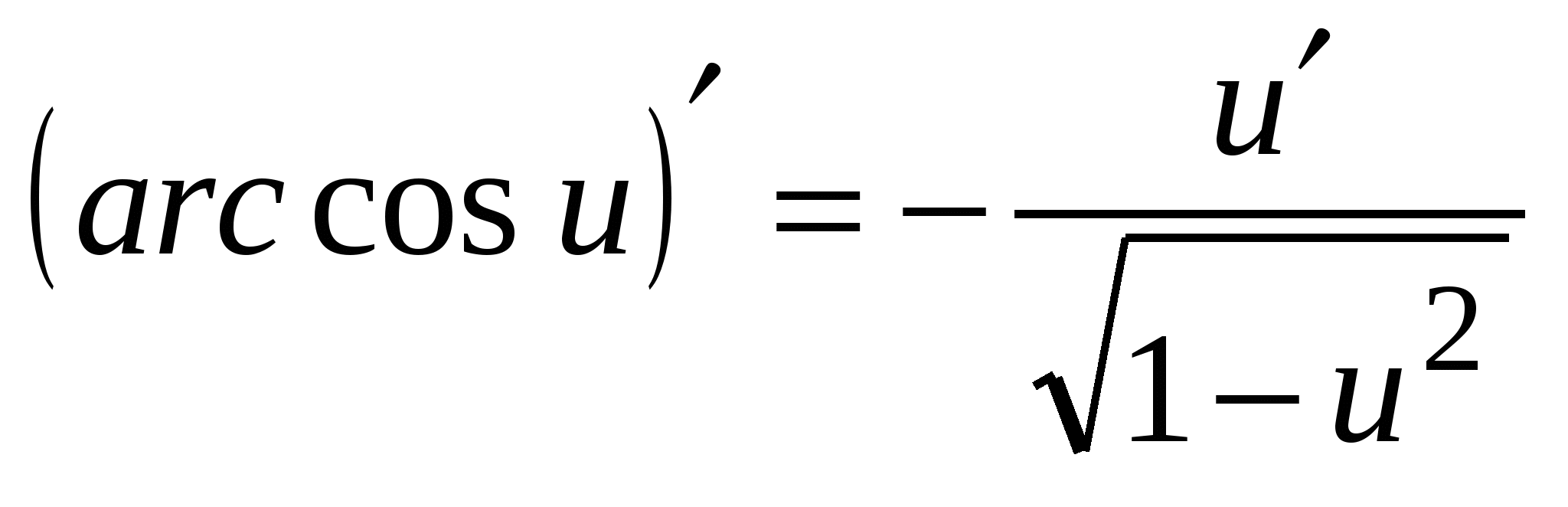
12. 
12. 
13. 
13. 
Ejemplos de revisión
Ejemplo 1.
y=(3-2 pecado 5x ) 4 | Aplicamos fórmulas derivadas para Y α , pecado tu |
y ¢ =4·(3–2·sen5x) 3·(3–2sen5x) ¢ =4·(3–2·sen5x) 3 ·(0–2·cos5x·5) = –40·(3–2·sen5x) 3 .
Ejemplo 2.
. 

Ejemplo 3.
 .
. 

Ejemplo 4.



Ejemplo 5.
 .
. 

Extremo de la función
El estudio de una función en un extremo es una de las aplicaciones más importantes de las derivadas. Veamos la definición de mínimos y máximos y cómo encontrarlos.
Sea la función ƒ( X) está definido y diferenciable en un determinado conjunto y un punto X 0 es un punto dentro de él.
Definición. Función ƒ (X) en el punto X 0 tiene máximo(mínimo), si existe tal vecindad del punto X 0, que es para todos X de esta zona ƒ (X) < ƒ (X 0 ) (ƒ (X) > ƒ (X 0 )).
Punto X 0 entonces se llama punto máximo(mínimo).

Arroz. 1.
Se muestra una gráfica de una función que tiene dos puntos máximos ( X 1 y X 3) y dos puntos mínimos ( X 2 y X 4), y el valor máximo puede ser menor que el mínimo ( ƒ (X 1 ) < ƒ (X 4)). Esto enfatiza el hecho de que caracterizamos la singularidad de una función solo cerca de cierto punto.
Los valores de la función en los puntos de máximo y mínimo se denominan valores extremos o extremos. El gráfico anterior muestra que los puntos extremos ( X 1 , X 2 , X 3 , X 4) determinar los intervalos de monotonía de la función, en cada uno de los cuales la derivada conserva un determinado signo. En los puntos extremos, por supuesto, la derivada tiende a cero. Formulemos un teorema sobre condición necesaria existencia de un extremo.
Teorema. Si la función ƒ (X) en el punto X 0 tiene un extremo, entonces la derivada de la función en este punto es igual a cero, es decir, ƒ¢ ( X 0)=0.
Observemos inmediatamente que esta condición no es suficiente, es decir, la afirmación inversa no siempre es cierta. Desde la igualdad ƒ ¢ ( X 0)= 0 no necesariamente sigue eso en el punto X 0 hay un extremo.
Esto se confirma con un ejemplo con la función ƒ (X)=x 3 .
Lo encontraremos ƒ ¢ ( X)= 3X 2 . En el punto X=0 ƒ ¢(0)=0 . Pero tan cerca del punto como quieras. X=0 encontraremos X> 0, donde ƒ (X)=x 3 > 0, lo encontraremos X< 0, где ¦ (X)=X 3 < 0. Т. е. не существует какая-либо малая окрестность точки X=0, donde para todos X valor de la función en un punto X=0 será el mayor o el menor. Por lo tanto punto X=0 no es un punto extremo.
Se puede argumentar de otra manera. Desde la derivada ƒ ¢ (x)=3x 2 , entonces la función f(x)=x 3 aumenta para cualquier x real y no tiene extremos.
Puntos en los que se cumple la condición extrema necesaria (ƒ ¢ (x)=0) son llamados crítico .
Obviamente, la tangente a la gráfica de la función en los puntos donde ƒ ¢ (x)=0, paralelo al eje x Ox .
Condición suficiente El extremo se da en los siguientes teoremas.
Teorema 1. Si X 0 es el punto crítico de la función y al pasar por él la derivada cambia de signo, entonces X 0 es un punto extremo, es decir, si la derivada cambia de signo de más a menos, es un punto máximo, y si cambia de signo de menos a más, es un punto mínimo.
Tenga en cuenta que no hay extremo en un punto si la derivada no cambia de signo. La regla para estudiar el extremo utilizando la primera derivada se conoce en el curso escolar. A veces es más conveniente formular una condición suficiente para un extremo utilizando la segunda derivada.
Sea la función ƒ( X) es dos veces diferenciable en algún dominio (es decir, ƒ( X) tiene ƒ¢ ( X) Y ƒ ¢¢ ( X)).
Teorema 2. Si X 0 – punto crítico de la función f(x) y ƒ ¢¢ (X 0 ) > 0 , Eso X 0 – punto mínimo, si ƒ ¢¢ (X 0 ) < 0, то X 0 – punto máximo.
Utilizando la segunda derivada se determina la convexidad o concavidad de la gráfica de una función.
Convexidad, concavidad. Punto de inflexión.
Curva y=ƒ(X) se llama convexamenteth abajo cualquiera de ella tangente
ƒ ¢¢ ( X) < 0.
Curva y=ƒ(X) se llama cóncavo en un intervalo si todos los puntos de la curva se encuentran más alto cualquiera de ella tangente en este intervalo. Entonces en este intervalo
ƒ ¢¢(x) > 0
Definición. Punto de inflexión Una curva es un punto donde por un lado la curva es convexa y por el otro es cóncava.
En el punto de inflexión ƒ ¢¢ ( X)=0.
Entonces, el signo de la segunda derivada (así como el signo de la función misma y su primera derivada) indica las características de la gráfica de la función. Veámoslos de nuevo.
si para todos X en el intervalo ( A, b) ƒ (X) > 0 (ƒ (X) < 0), entonces la gráfica se encuentra encima (debajo) del eje x.
si para todos X en el intervalo ( A, b) ƒ ¢ ( X) > 0 (ƒ ¢ ( X) < 0), то функция на (A, b) aumenta (disminuye).
si para todos X en el intervalo ( A, b) ƒ ¢¢ ( X) > 0 (ƒ ¢¢ ( X) < 0), то график на (A, b) cóncavo convexo).
Ecuación ƒ( X)=0 define los “ceros” de la función, es decir, los puntos de intersección de la gráfica con el eje Ox.
La ecuacion ƒ ¢ ( X)=0 define puntos críticos.
La ecuacion ƒ ¢¢ ( X)=0 define posibles puntos de inflexión.
Esquema de estudio de funciones
Para estudiar la función. ƒ (X) y trazando y=ƒ(X) se debe encontrar:
1) el dominio de definición de la función y el punto de intersección del gráfico con los ejes de coordenadas;
2) intervalos de monotonía;
3) puntos de extremos y valores de función en estos puntos;
4) intervalos de convexidad y concavidad del gráfico;
5) puntos de inflexión del gráfico;
6) construir en un sistema de coordenadas cartesiano todos los puntos obtenidos (a veces, para aclarar la gráfica, se obtienen puntos adicionales) y la gráfica misma.
Los valores más pequeños y más grandes de una función en un segmento.
Al resolver algunos problemas del método de optimización, es importante poder encontrar los valores más pequeños o más grandes de una función en un segmento determinado. La función alcanza estos valores ya sea en puntos críticos o en los extremos del segmento.
Esquema de búsqueda los valores más pequeños y más grandes de la función ƒ (X) en el segmento [ A, b].
1. Encuentra la derivada de la función. ƒ ¢ ( X).
2. Encuentra los puntos críticos de la ecuación. ƒ ¢ ( X)=0.
3. Seleccione aquellos puntos críticos que pertenecen a este segmento [ A, b] y encontrar el valor de la función ƒ (X) en cada uno de esos puntos.
4. Calcular los valores de las funciones. ƒ (X) en los extremos del segmento: ƒ( A) y ƒ( b).
5. De los valores de función obtenidos, seleccione el más grande (más grande) y el más pequeño (más pequeño).
Ejemplo 2.
Encuentra los valores mayor y menor de una función. f(x)=X 3 –9x 2 +24х–10 en el segmento.
1. ƒ ¢ ( X)= 3X 2 – 9·2 X 2 + 24.
2. ƒ ¢ ( X)=0, 3(X 2 –6X+8)=0, X 1 =2, X 2 =4.
3. El punto x 2 =4 no pertenece al segmento. Por lo tanto, calculamos el valor de la función solo en el punto X 1 =2
ƒ(2)=2 3 –9·2 2 +24·2–10=10.
4. Valores de función en los extremos del segmento: ƒ(0)= –10, ƒ(3)=3 3 –9·3 2 +24·3–10, ƒ(3)=8.
5. Valores obtenidos:
ƒ(2)=10, ƒ(0)= –10, ƒ(3)=8.
El valor más alto es 10 y se alcanza en el punto X=2. El más pequeño es igual a –10 y se alcanza en el punto X=0.
Ejemplo 3.
Encuentre los intervalos de convexidad y concavidad y los puntos de inflexión de la curva. y=x+36X 2 –2X 3 –X 4 .
El dominio de definición de esta función es el conjunto de todos los números reales, es decir XЄ(–∞, +∞).
Encontremos la segunda derivada.
en¢=1+72 X–6X 2 –4X 3 .
en¢¢ =72–12 X–12X 2 = –12(X 2 +X–6).
De la ecuación. en¢¢ =0 obtenemos la abscisa del punto de inflexión:
–12(X 2 +X–6)=0 X 1 = –3; X 2 =2.
Definamos el signo en¢¢ en intervalos
(–∞; –3), (–3; 2), (2, +∞).
X
(–∞, –3)
(–3; 2)
(2; +∞)
en¢¢
forma de curva
convexo
inflexión
cóncavo
inflexión
convexo
Encontremos las ordenadas de los puntos de inflexión:
en(–3)=726; METRO 1 (–3; 726) – punto de inflexión
en(2)=114; METRO 2 (2; 114) – punto de inflexión.
En el intervalo (–3; 2) la curva es cóncava. En los intervalos (–∞; –3) y (2; +∞) – convexos.
Ejemplos de tareas
Tarea número 1.
Encuentra los puntos de interrupción de la función y traza la gráfica.

Función ƒ (X) está definido para todo real X y es continua en cada uno de los intervalos indicados: (–∞; –1), [–1; 0], (0, +∞). Exploremos la función ƒ (X) para la continuidad en puntos X= –1 y X=0.
Para ello encontraremos límites unilaterales en cada uno de estos puntos.

Dado que los límites unilaterales son diferentes, entonces X = –1 – punto de discontinuidad del primer tipo.

Los límites unilaterales son iguales, es decir, en el punto x=0 hay un límite de la función y 
Comparemos este límite con el valor de la función en el punto: 
Porque  luego en en x=0 la función ƒ(x) es continua.
luego en en x=0 la función ƒ(x) es continua.
Tracemos la función ƒ (X), dado que
1)  – ecuación de una línea recta,
– ecuación de una línea recta,
2)  – ecuación del semicírculo superior
– ecuación del semicírculo superior  con centro en el origen y radio igual a la unidad, y bajo la condición –1 £ X£ 0 ecuación
con centro en el origen y radio igual a la unidad, y bajo la condición –1 £ X£ 0 ecuación  define un cuarto de círculo.
define un cuarto de círculo.
3) para X > 0 la gráfica viene dada por la ecuación  . Encontramos los puntos de intersección de esta curva con el eje Ox de la ecuación
. Encontramos los puntos de intersección de esta curva con el eje Ox de la ecuación  para x > 0. x= π
norte, Dónde norte
=1, 2, 3, 4,
para x > 0. x= π
norte, Dónde norte
=1, 2, 3, 4,

Arroz. 2.
Tarea número 2.
Escribir ecuaciones para tangentes a una recta.  en puntos donde X=0 y X=4. Encuentra el punto de intersección de las tangentes y el ángulo entre ellas. Haz un dibujo.
en puntos donde X=0 y X=4. Encuentra el punto de intersección de las tangentes y el ángulo entre ellas. Haz un dibujo.
Ecuación de una tangente a una recta. y=ƒ(x) parece
Dónde en 0 =ƒ( X 0).
En el punto X=0 en(0)=ƒ(0)=5.
en¢ =ƒ ¢ (X)=X–3 ƒ¢ (0)= –3.
METRO 1 (0, 5) tiene la forma y– 5= –3(X–0) o
y= –3X+5.
En el punto X=4 en(4)=ƒ(4)=1. ƒ¢ (4)=4–3=1.
Ecuación de una tangente en un punto. METRO 2 (4, 1) tiene la forma y– 1=X–4 o
y=x–3.
Obtenemos el punto de intersección de las tangentes resolviendo el sistema

Punto de intersección METRO 3 (2, –1).
Esquina φ entre tangentes encontramos de la fórmula:
 ,
,
Dónde k 1 = –3; k 2 =1 – coeficientes angulares de tangentes.
 .
.
Esquina φ = arco 2.
Construyamos esta línea  – una parábola con un vértice en el punto donde X=3, porque en¢
=0 en X=3. Lo encontraremos
– una parábola con un vértice en el punto donde X=3, porque en¢
=0 en X=3. Lo encontraremos  . Punto METRO 4 (3;
. Punto METRO 4 (3;  ) es el vértice de la parábola.
) es el vértice de la parábola.
R 
es. 3.
Tarea número 3.
Función de exploración 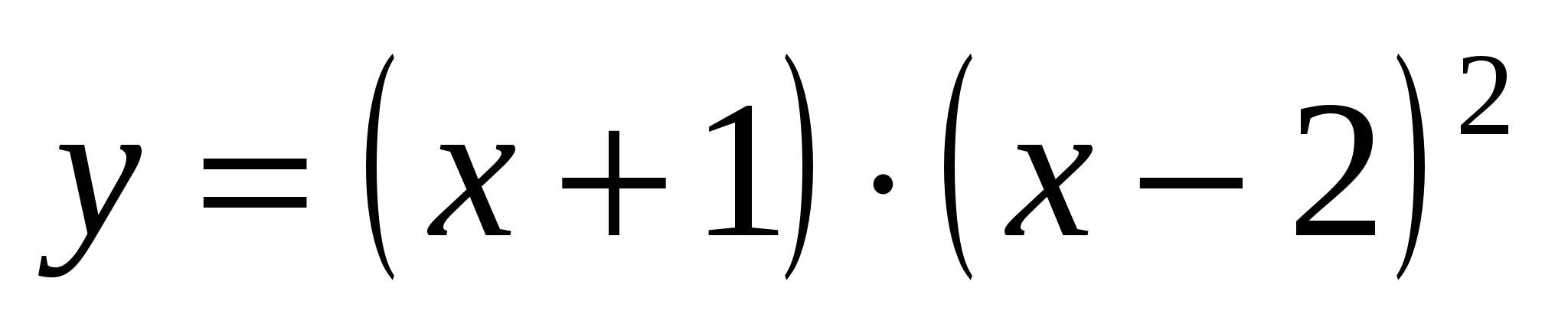 y trazarlo.
y trazarlo.
1. Esta función es un polinomio (puedes abrir los paréntesis, obtenemos un polinomio de tercer grado), por lo tanto es definida, continua y diferenciable para cualquier X.
2. Encontremos la derivada.
 .
.
De la ecuación. en¢ =0 busquemos puntos críticos: 3 X·( X–2)=0, X 1 =0, X 2 =2.
Exploremoslos.
X
(–∞, 0)
(0; 2)
(2; +∞)
en ¢
en
3. Entonces, la función aumenta en los intervalos (–∞, 0) y (2, +∞), disminuye en el intervalo (0; 2), tiene un máximo en x=0 y un mínimo en x=2:
en máximo = en(0)=4; en mín = en(2)=0.
4. Encontremos la segunda derivada.
en¢¢ = 6·( X-1).
La curva es convexa donde en¢¢ < 0, т. е. 6·(X–1) < 0, X < 1.
La curva es cóncava donde en¢¢ > 0, es decir X > 1.
Entonces, en el intervalo (–∞, 1) la curva es convexa; y en el intervalo (1, +∞) es cóncavo.
5. Encontramos el punto de inflexión de la ecuación. en¢¢ =0. De este modo, X=1 – abscisa del punto de inflexión, porque este punto separa los intervalos de convexidad y concavidad de la curva. Ordenada del punto de inflexión: en(1)=2.
Gráfica de una función en=(X+1)·( X–2) 2 cruza el eje Ox en en=0, es decir, cuando X= –1 y X=2;
cruza el eje Oy en X=0, es decir, cuando en=4. Obtuvimos tres puntos: (–1; 0), (2; 0), (0; 4). Introduciremos en la tabla todos los puntos obtenidos sumando los adyacentes a ellos.
–2
–1



–16


es. 4 Curva y=(x+1)(x–2) 2.
Tarea número 1
Te presentamos tareas que pueden tener una, dos, tres o más respuestas correctas. Encierra en un círculo los números de todas las respuestas correctas.
1. Si  entonces la función
entonces la función
1) aumentando
2) decreciente
3) constante
2. Si
1) creciente
2) Decreciente
3. Si  , entonces la función
, entonces la función
1) creciente
2) Decreciente
4. Si  , entonces la función
, entonces la función
1) Creciente 3) Decreciente
2) Constante 4) Monótono
5. Función  Es
Es
1) Incluso
2) Ni siquiera
3) ni par ni impar
4) periódico
5) No periódico
6) trigonométrico
7) Primaria
6. Función  Es
Es
1) incluso
2) impar
3) ni par ni impar
4) periódico
5) no periódico
6) trigonométrico
7) elemental
2) Weierstrass 4) Dirichlet 6) Leibniz
8) Solución  Ecuaciones
Ecuaciones
1) 0 3) 0 y 3 5) 2 7) 3
2) 2 y 3 4) 2 6) -5 y 1 8) 5 y 1
9) solución a la desigualdad 
1) ( ; 1) 3) (
; 1) 3) ( ; 1) 5) (-
; 1) 5) (- ;1)
;1)
2) (1; 5) 4) (2;  ) 6)
) 6) 
10) Método  La cantidad se encuentra
La cantidad se encuentra
1) vectores
2) recto
3) segmento
11) Si  , entonces la función
, entonces la función
1) Cóncavo 3) Convexo 5) Decreciente
2) Monótono 4) Creciente 6) Constante
12) el dominio de definición de la función es igual a 
1) ( ;0)
;0)
2) (0;  )
)
3) (- ;
; )
)
4) (0;1)
5) 
6) 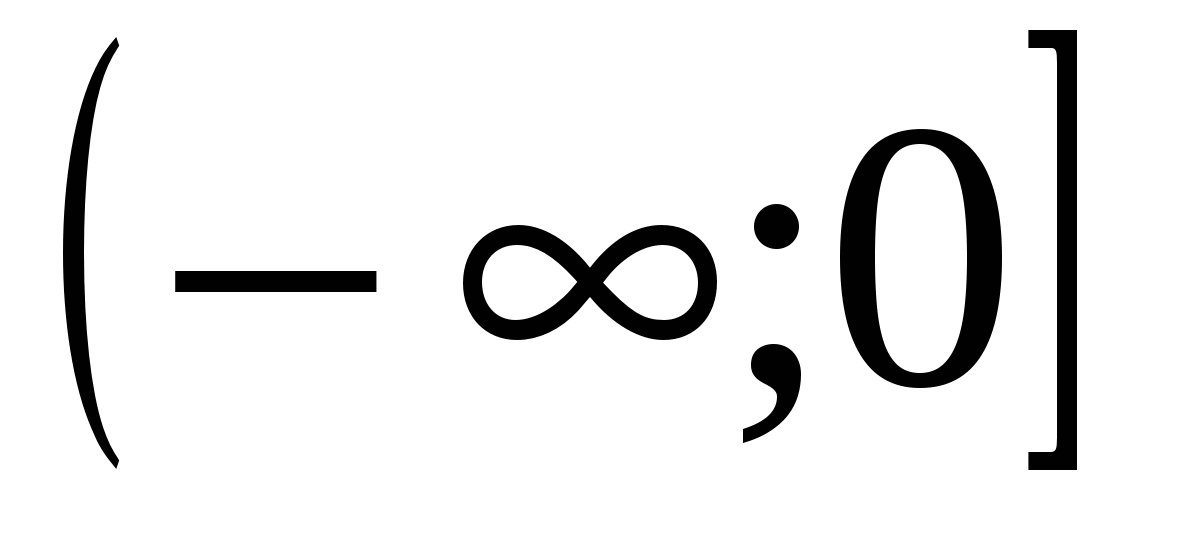
7) (-1;1)
8) 
9) 
13) función  es
es
1) indicativo
2) trigonométrico
3) poder
4) logarítmico
14) si funciones y = X  entonces ella es
entonces ella es 
1) incluso
2) impar
3) ni par ni impar
15) función  en
en  es
es
Objetivos de la lección:
Educativo- conocer fórmulas de diferenciación; reglas de diferenciación;
diferenciación de una función compleja; significado físico y geométrico de derivada;
ecuación de la tangente a la gráfica de una función.
Desarrollo - ser capaz de encontrar derivadas de funciones; resolver problemas utilizando significado físico, significado geométrico; encontrar el valor de la derivada de una función en un punto; Explicar y justificar matemáticamente correctamente las acciones realizadas.
Educativo – cultivar la independencia, la responsabilidad, la reflexión.
durante las clases
I. Momento organizativo.
II. revisando la tarea
(durante los recesos, los consultores verifican (a los estudiantes) y asignan calificaciones).
III. Establecimiento de objetivos y motivación.
El profesor informa a los estudiantes que esta lección es la última lección sobre el tema "Cálculo de derivadas" y los invita a formular sus propios objetivos.
Maestro: “El gran filósofo Confucio dijo una vez: “Tres caminos conducen al conocimiento: el camino de la reflexión es el camino más noble, el camino de la imitación es el camino más fácil y el camino de la experiencia es el camino más amargo”. Así que hoy en clase cada uno de ustedes determinará en qué camino hacia el conocimiento de este tema se encuentra”.
A los estudiantes se les asigna la tarea de demostrar sus conocimientos y habilidades para calcular derivadas y se les proporciona un plan de lección.
Etapa I: Completar la tarea usando la tarjeta "Recordar".
(prueba de conocimiento de fórmulas y reglas de diferenciación).
Etapa II: Trabajo frontal oral sobre repetición y generalización de conocimientos.
Etapa III:“Pronóstico de prueba” (al realizar esta tarea, la ayuda de consultores es aceptable).
IEtapa V: Solución de un problema práctico.
Etapa V: Trabajo independiente
Se evalúan las etapas I, III, V de trabajo y tareas. Los consultores verifican e ingresan los resultados en la tabla de evaluación.
Criterios de evaluación: "5"- 19-20 puntos;
"4"- 15-18 puntos;
"3"- 10-14 puntos.
Caminos al conocimiento
- Reproducción y corrección de conocimientos de referencia.
Etapa I.
Objetivo: control, autocontrol del conocimiento de fórmulas y reglas de diferenciación
¡Recordar! FI ___________________________________________________ |
|
Derivado |
|
c,c - contras t |
|
|
|
|
|
F"(x)+ gramo"(X) |
|
F(X)* gramo(X) |
|
|
|
Al finalizar esta tarea, se realiza una autoprueba utilizando la “Tabla de Derivados”. Las tarjetas se entregan a consultores para su verificación (no se permiten correcciones en las tarjetas).
V. Generalización y sistematización del conocimiento.
Etapa II.
1. Trabajo frontal oral.
A. Genera una tarea para esta condición y resuélvela.
![]()
1. Encuentre el valor de la derivada de la función en el punto t = 3. (Respuesta: 21.)
2. Crea una ecuación para la tangente a la gráfica de la función en el punto t = 3. (Respuesta: y = 21x-45.).
3. Calcula la velocidad del cuerpo y la aceleración en el momento t=3c, si la ley del movimiento viene dada por la fórmula. (Respuesta: 21 m/s, 16 m/s²).
4. Encuentre el coeficiente angular de la tangente trazada a la gráfica de la función en el punto t = 3. (Respuesta: 21.).
5. Encuentre la tangente del ángulo de inclinación de la tangente a la gráfica de la función en el punto t = 3 y determine el tipo de ángulo entre la tangente y la dirección positiva del eje Ox. (Respuesta: tgα, el ángulo α es agudo)
B. Encontrar derivadas de funciones.

2. Etapa III“Pronóstico de prueba”


Al final de esta tarea, se realiza una autoevaluación basada en las respuestas finales y las pruebas se entregan a los consultores. (No se permiten correcciones en las tarjetas).
Respuestas:
1 opción |
||||
opcion 2 |
- La solución del problema
IEtapa V
Solución frontal a un problema de nivel avanzado (la solución la realizan consultores junto con la clase).
Tarea
¿En qué valores de parámetros? a tangentes a la gráfica de una función ![]()
dibujados en los puntos de su intersección con el eje X, forman entre sí un ángulo de 60°?

La gráfica es una parábola con ramas ascendentes que cortan el eje X en dos puntos (el caso a=0 no satisface el significado del problema):
IX. Resumir y calificar
1. Preguntas: a) ¿Se ha logrado el propósito de la lección?
b) ¿Qué etapa le pareció la más difícil?
c) ¿Qué fue lo más interesante?
2. Los consultores anuncian los resultados (número y nombres de los estudiantes en camino).
imitación, modos de reflexión y modos de experiencia).

 .
.