Izpeljanka teme praktične lekcije številka 9. Praktična lekcija "izračun derivatov"
Praktično delo
matematika
1. Iskanje limita funkcije. Prva in druga sta čudoviti meji.
2. Odvod kompleksne funkcije. Preučevanje funkcije ene spremenljivke in risanje grafov.
3. Test "Uporaba diferencialnega računa pri študiju funkcij."
4. Iskanje nedoločenih integralov. Računanje določenih integralov.
5. Izračun determinant.
6. Reševanje sistemov linearnih enačb po Cramerjevi metodi. Test.
7. Reševanje problemov na temo "Množice". Formule logične algebre.
8. Izračun verjetnosti naključnih dogodkov. Formula skupne verjetnosti.
9. Izračun numeričnih karakteristik.
10. Test "Osnove teorije verjetnosti in matematične statistike"
11. Trigonometrična oblika kompleksnega števila.
12. Dejanja s kompleksnimi števili v različnih oblikah.
METODIČNA NAVODILA ZA PRAKTIČNO DELO PRI MATEMATKI
TEČAJ 2
Praktični pouk je oblika organizacije izobraževalnega procesa, ki vključuje študente, ki opravljajo eno ali več praktičnih del po nalogu in pod vodstvom učitelja.
Tako dijaki pri praktičnem pouku matematike razvijajo zmožnost reševanja problemov, ki naj bi jih v prihodnje uporabili pri reševanju strokovnih problemov v specialnih disciplinah.
Med praktičnim delom študenti obvladajo sposobnost uporabe virov informacij, delo z regulativnimi dokumenti in učnimi gradivi, referenčnimi knjigami, izdelavo risb, diagramov, tabel, reševanje različnih vrst problemov in izračune.
Problemi, ki se rešujejo pri praktičnem pouku matematike:
1) razširitev in utrjevanje teoretičnega znanja matematike, pridobljenega pri predavanjih;
2) razvijanje praktičnih spretnosti in spretnosti pri učencih, potrebnih za uspešno reševanje matematičnih problemov;
3) razvoj potrebe študentov po samoizobraževanju in izpopolnjevanju znanja in spretnosti v procesu študija matematike;
4) oblikovanje ustvarjalnega odnosa in raziskovalnega pristopa v procesu študija matematike;
5) oblikovanje strokovno pomembnih lastnosti bodočega strokovnjaka in spretnosti pri uporabi pridobljenega znanja na poklicnem področju.
Praktična lekcija št. 1. Izračun funkcijskih mej. Prva in druga sta čudoviti meji.
Predmet : Izračun funkcijskih mej.
Cilj: pridobitev osnovnih znanj s področja temeljnih vej matematike . Preverjanje asimilacije znanja o izračunu limitov funkcij. Ponovite in sistematizirajte znanje o tej temi.
Naloge:
Razvoj kreativnega poklicnega mišljenja;
Obvladovanje znanstvenega jezika, veščine operiranja s koncepti;
Obvladovanje veščin postavljanja in reševanja problemov;
Poglabljanje teoretičnega in praktičnega usposabljanja;
Razvoj pobude in samostojnosti študentov.
Krepitev računalniških veščin;
Nadaljujte z delom na matematičnem govoru.
Oblikovanje spretnosti za samostojno delo, delo z učbenikom, spretnosti za samostojno pridobivanje znanja;
Razvoj sposobnosti poudarjanja glavne stvari pri delu z besedilom;
Oblikovanje samostojnega mišljenja, miselnih operacij: primerjava, analiza, sinteza, posplošitev, analogija;
Učencem predstaviti vlogo sistematičnega dela pri poglabljanju in krepitvi znanja, o kulturi izpolnjevanja nalog;
Razvoj ustvarjalnih sposobnosti učencev.
Zagotavljanje praktičnega dela:
Teoretično gradivo metodoloških priporočil za praktično delo.
Matematika, – Zbirka: Srednje poklicno izobraževanje. - Rostov na Donu "Feniks", str.
Potek praktičnega pouka.
1. Oblikovanje teme lekcije, razlaga povezave teme z drugimi temami akademske discipline;
2. Preverjanje pripravljenosti učencev za pouk;
3. Izvedba samega pouka glede na temo in v skladu z delovnim programom discipline:
Preučite teoretično gradivo na temo "Izračunavanje meja funkcij."
Razmislite o primerih reševanja tipičnih nalog.
Opravite samostojno delo pri izračunavanju limitov funkcij z uporabo prve in druge izjemne limite.
Odgovori na varnostna vprašanja.
Teoretične informacije in metodološka priporočila
pri reševanju problemov.
1. Predstavitev teoretičnega gradiva.
Če želite izračunati limit funkcije v točki, morate:
1) Namesto spremenljivke x zamenjajte tisto, h čemur teži x.
2) Če po zaključku koraka 1) dobimo negotovost v obliki https://pandia.ru/text/78/405/images/image003_6.png" width="19" height="22 src=">in zamenjamo puščica z minusom: (x-a).
3) Če po zaključku 1. koraka prejmemo negotovost v obliki https://pandia.ru/text/78/405/images/image002_13.png" width="18" height="31 src="> povezanih z vrednostmi trigonometričnih funkcij, moramo uporabiti prvo izjemno mejo.
Opredelitev. Prva izjemna meja se imenuje meja
https://pandia.ru/text/78/405/images/image007_4.png" alt="$\displaystyle \lim_(x\to0)\dfrac(\sin x)(x)=1. $" width="102" height="52">!}
5) definicija:Druga izjemna meja imenovana meja

Število, ki ga daje ta meja, ima zelo pomembno vlogo tako v matematični analizi kot v drugih vejah matematike. Številka je poklicana osnova naravnih logaritmov ( https://pandia.ru/text/78/405/images/image009_4.png" alt="$ e$" width="11" height="14">показывает, что -- иррациональное число, несколько первых десятичных знаков которого таковы:!}
![]()
2. Utrjevanje preučenega gradiva.
Primer 1
https://pandia.ru/text/78/405/images/image015_1.png" width="28" height="30 src=">= -4
Uporabili smo pravilo 1) in namesto x nadomestili tisto, h čemur naj x teži, tj. x=2.
Primer 2
https://pandia.ru/text/78/405/images/image017_1.png" width="154" height="32 src=">.png" width="21" height="30 src=">= 5
Primer 3
https://pandia.ru/text/78/405/images/image021_1.png" width="199" height="37 src=">.png" width="137" height="35 src=">. png" width="138" height="24 src=">=3+3=6
Primer 4
https://pandia.ru/text/78/405/images/image004_7.png" width="22" height="31 src=">.png" width="104" height="46 src=">. png" višina="30 src=">
Primer 5
https://pandia.ru/text/78/405/images/image032_0.png" width="61" height="46 src=">.png" height="30 src=">=2
Primer 6
https://pandia.ru/text/78/405/images/image036_0.png" width="18" height="28 src=">
b) 
V) 
3. Utrjevanje znanja, spretnosti in spretnosti.
Samostojno se lotite računanja limitov funkcij.
Praktično delo št. 1. Možnost 1 Izračunaj limito funkcije: 1. 2. 3. 10. | Praktično delo št. 1. Možnost 2 Izračunaj limito funkcije: 1. 2. 3. 10. |
Praktično delo št. 2.
Predmet : Iskanje odvoda funkcije. Preučevanje funkcije ene spremenljivke in risanje grafa.
Tarča : Preveri v praksi poznavanje pojma odvod funkcije, sposobnost iskanja odvodov elementarnih funkcij, kompleksnih funkcij, inverznih funkcij, uporaba tabele odvodov in pravil diferenciranja, pojma kompleksne in inverzne funkcije, zmožnost uporabiti derivat za preučevanje funkcij.
Zagotavljanje praktičnega dela:
Učbenik. "Matematika". – M.: Bustard, 2010.
Matematika. M: Forum-Infa 2008.
Individualne karte z možnostjo praktičnega dela.
1. Teoretično gradivo in primeri iskanja odvoda funkcije.
definicija: Odvod funkcije f(x) (f"(x)) v točki x je meja razmerja med prirastkom funkcije in prirastkom argumenta, ko se prirastek argumenta nagiba k ničli:
https://pandia.ru/text/78/405/images/image061_0.png" width="209 height=235" height="235">
Pravila razlikovanja.
Če imata funkciji f(x) in g(x) odvode, potem
2. (u+v)′=u′+v′
3. (uv)′=u′v+v′u
4. (C u)′=C u′, kjer je C=const
5..png" width="49" height="54 src=">
6. Izvod kompleksne funkcije:
f′(g(x))=f′(g) g′(x)
2. Primeri.
1..png" width="61" height="41 src=">.png" width="20" height="41 src=">.png" width="20" height="41 src="> .png" width="69" height="41 src=">+4).
Funkcija je produkt dveh faktorjev: u=https://pandia.ru/text/78/405/images/image071_0.png" width="72" height="41 src=">.png" width=" 64" height="41 src=">.png" width="19" height="41 src=">.png" width="45" height="51 src=">.
Funkcija je količnik dveh izrazov: u=https://pandia.ru/text/78/405/images/image079.png" width="52" height="41 src=">..png" width= "215" " height="57 src=">.png" width="197 height=36" height="36">
rešitev. Poiščimo odvod te funkcije z uporabo pravila diferenciacije kompleksnih funkcij (formula 6):

5. Če , potem 
6. l = x 3 – 3x 2 + 5x+ 2. Poiščimo l "(–1).
l " = 3x 2 – 6x+ 5. Zato, l "(–1) = 14.
7. če l= dnevnik x cos x, To l" = (ln x)"ker x+ln x(ker x) " =1/x∙cos x–ln x greh x.
Naj bo dana funkcija. Za študij potrebujete:
1) Poiščite njegovo definicijsko domeno. Če ni pretežko, je koristno najti tudi obseg. (Vendar se v mnogih primerih vprašanje iskanja odloži, dokler se ne najdejo ekstremi funkcije.)
2) Ugotovite splošne lastnosti funkcije, ki vam bodo pomagale pri določanju njenega obnašanja: ali je funkcija soda ali liha, ali je periodična.
3) Ugotovite, kako se funkcija obnaša, ko se argument približa mejnim točkam definicijskega področja, če te mejne točke obstajajo. Če ima funkcija diskontinuitetne točke, je treba te točke preveriti tudi glede prisotnosti navpičnih asimptot funkcije. Poiščite poševne asimptote.
4) Poiščite presečišča grafa s koordinatnimi osmi, kar je sestavljeno iz preprostega izračuna vrednosti funkcije pod pogojem:
Z osjo OX: y=0;
Z osjo OY: x=0.
Iskanje presečišč z osjo lahko vodi do potrebe po reševanju zapletene algebrske enačbe, kar je morda mogoče storiti le približno. Ko najdemo korenine funkcije in diskontinuitetne točke, lahko določimo znak funkcije na vsakem od intervalov med temi točkami. To je mogoče storiti z izračunom vrednosti funkcije na kateri koli točki v intervalu ali z uporabo intervalne metode.
5) Poiščite intervale monotonosti. Če želite to narediti, poiščite odvod in rešite neenačbo:
https://pandia.ru/text/78/405/images/image089.png" width="49" height="19 src=">, funkcija se zmanjšuje.
Ko najdemo intervale monotonosti, lahko takoj določimo točke lokalnega ekstrema: kjer se povečanje zamenja z zmanjšanjem, se nahajajo lokalni maksimumi, in kjer se zmanjšanje zamenja s povečanjem, se nahajajo lokalni minimumi.
6) Iskanje intervalov konveksnosti in konkavnosti se izvede z uporabo drugega odvoda..png" width="39" height="19 src="> na intervalih:
če https://pandia.ru/text/78/405/images/image090.png" width="39" height="19 src=">‹0, potem je krivulja funkcijskega grafa konveksna.
Hkrati definiramo prevojne točke kot tiste točke, v katerih funkcija spremeni smer konveksnosti (in je zvezna).
7) Iskanje presečišč grafa z asimptoto in dodatnimi točkami. Ta točka ni obvezna, vendar je z iskanjem takih točk študija funkcije in njenega grafa popolna in popolna.
Upoštevajte, da je koristno takoj narisati točke na koordinatnih oseh in na grafu, ki jih dobite med študijem funkcij na risbi. To pomaga razumeti videz grafa na poti.
3. Naredi sam:
|
možnost | Poiščite odvod funkcije y: |
možnost | Poiščite odvod funkcije y: |
1.y=6- | 1. y=-6- 5.y= |
||
1. y=-7-1 | 1. y=-7-1 |
||
1.y=4x-3tgx+6x-8 | 1.y=-5x+2ctgx+3x-2 |
||
Praktična lekcija
Zadeva: Iskanje izpeljank. Uporaba odvoda za preučevanje funkcij in risanje grafov.
Cilj: Obvladajte izračun odvodov, naučite se raziskovati funkcijo z uporabo odvoda
Sredstva izobraževanja: zvezki za praktične vaje, predstavitve na temo, internetni viri.
1. Upoštevajte teoretično gradivo na teme: »Pravila za izračun odvodov«, »Ekstremum funkcije«, »Konveksnost, konkavnost. Prevojna točka."
2. Preglejte vzorce nalog.
3. Izpolnite testno nalogo št. 1.
Kontrolna vprašanja:
1. Definirajte maksimum (minimum) funkcije v točki. Kaj lahko rečemo o predznaku prirastka funkcije v dokaj majhni okolici največje (minimalne) točke?
2. Kateri so nujni pogoji za obstoj ekstrema funkcije? Kakšen je njihov geometrijski pomen?
3. Kakšno je pravilo za iskanje največjih in najmanjših vrednosti funkcije na segmentu?
4. Določite konveksnost (konkavnost) krivulje na intervalu.
5. Kakšno je pravilo za iskanje intervalov konveksnosti in konkavnosti krivulje?
6. Prevojna točka krivulje. Kako jo najti?
7. Kakšen je algoritem za izdelavo grafa funkcije?
Pravila za izračun izvedenih finančnih instrumentov
Odvod kompleksne funkcije.
če pri=ƒ( in), u=φ(x), potem pri¢ ( X)=ƒ¢ (i)·φ¢ (X).
Izpeljanka vsote.
če pri(X)=in(X)+v (X), to pri¢ (X)=in¢ (X)+v ¢ (X)
Izpeljanka izdelka.
če y(x)=u(X)· v (X), to pri¢ = in¢ · v + u · v ¢ .
Še posebej, ( z· in)¢ =c· in¢, tj. konstantni faktor je vzet izpod predznaka za izpeljavo. To je enostavno preveriti
(u 2 ) ¢ = 2 u·u ¢ , (u 3 ) ¢ =3u 2 u ¢ , … , (u n ) ¢ =n·u n–1 u ¢ .
Izpeljanka količnika.
Če, potem  .
.
Tabela izvedenih finančnih instrumentov
1. (z)¢ =0
Za kompleksno funkcijo: če u=u(x), to:
2. (X)¢ =1
3. (X α )¢ = α · Xα–1, A– poljubno realno število.
 .
.
3. 

4. (A X ) ¢ =a X · ln A
4. 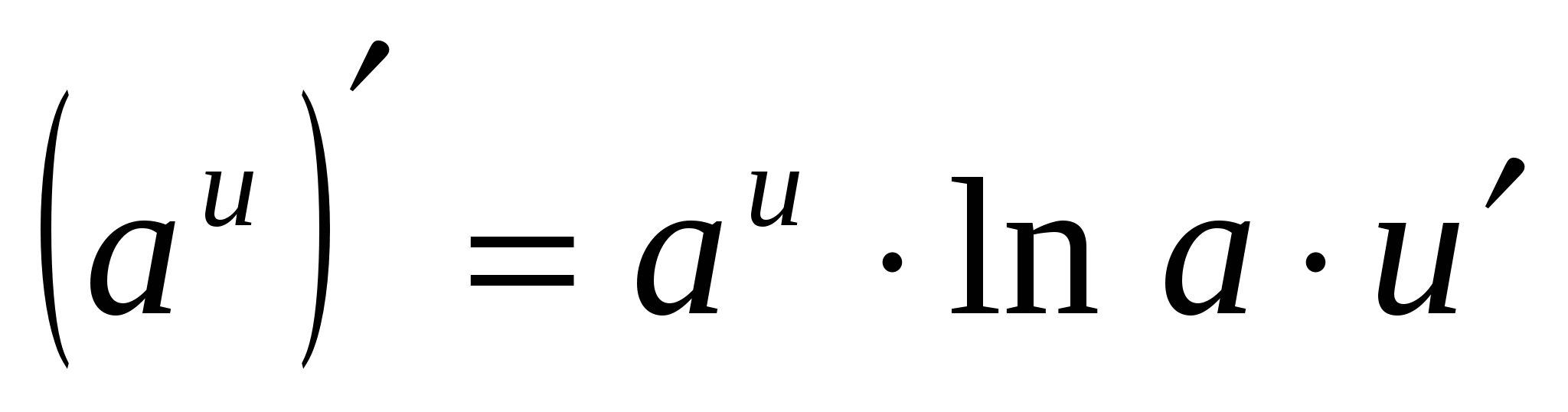

5. (dnevnik
a
x)
¢
=
 .
.
5. 

6. (greh x)¢ =cos x
6. 
7. (cos x)¢ = –sin x
7. 
8. (tg x)¢
=
8. 
9. (ctg x)¢
=
9. 
10. 
10. 
11. 
11. 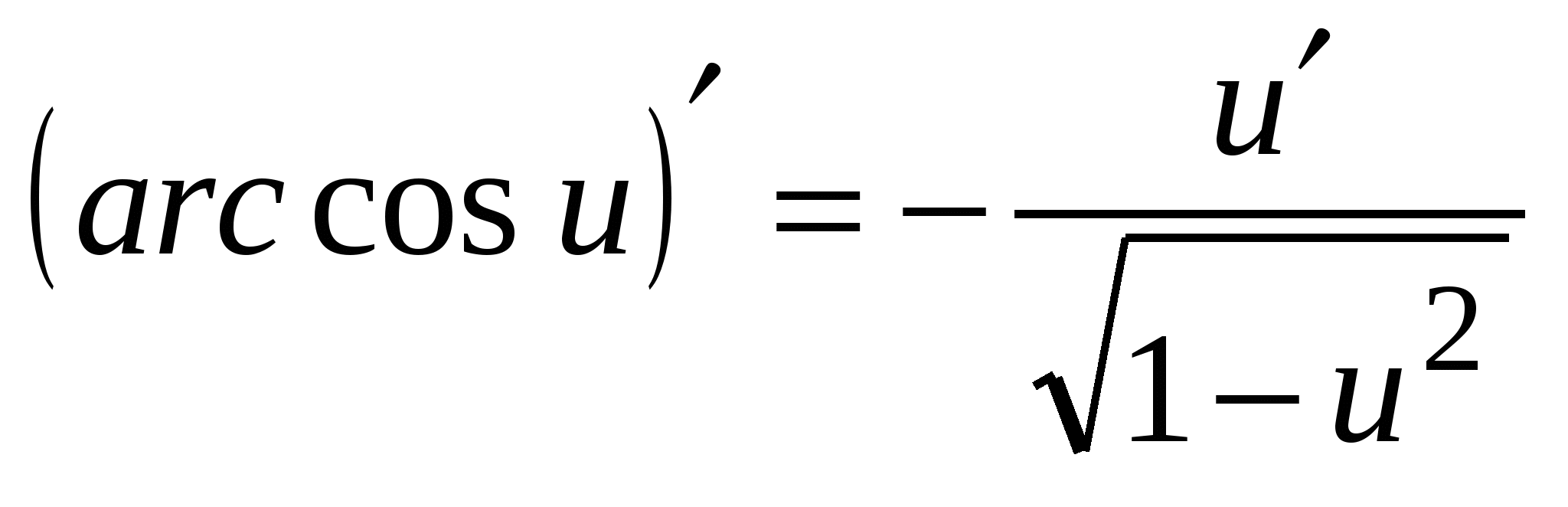
12. 
12. 
13. 
13. 
Pregled primerov
Primer 1.
y=(3–2 greh 5x ) 4 | Uporabljamo izpeljane formule za in α ,greh u |
l ¢ =4·(3–2·sin5x) 3·(3–2sin5x) ¢ =4·(3–2·sin5x) 3 ·(0–2·cos5x·5) = –40·(3–2·sin5x) 3 .
Primer 2.
. 

Primer 3.
 .
. 

Primer 4.



Primer 5.
 .
. 

Ekstrem funkcije
Preučevanje funkcije v ekstremumu je ena najpomembnejših aplikacij odvodov. Oglejmo si definicijo minimumov in maksimumov ter kako ju najti.
Naj funkcija ƒ( X) je definirana in diferencibilna na določeni množici in točki X 0 je točka znotraj njega.
Opredelitev. funkcija ƒ (X) na točki X 0 ima maksimum(najmanj), če obstaja taka soseska točke X 0, ki je za vse X s tega območja ƒ (X) < ƒ (X 0 ) (ƒ (X) > ƒ (X 0 )).
Pika X 0 se potem imenuje točka maksimum(najmanj).

riž. 1.
Prikazan je graf funkcije, ki ima dve največji točki ( X 1 in X 3) in dve minimalni točki ( X 2 in X 4), največja vrednost pa je lahko manjša od najmanjše ( ƒ (X 1 ) < ƒ (X 4)). To poudarja dejstvo, da karakteriziramo singularnost funkcije le v bližini določene točke.
Vrednosti funkcije v točkah maksimuma in minimuma imenujemo ekstremne vrednosti oz skrajnosti. Zgornji graf kaže, da sta ekstremni točki ( X 1 , X 2 , X 3 , X 4) določite intervale monotonosti funkcije, v vsakem od katerih derivat ohrani določen znak. V ekstremnih točkah gre seveda odvod na nič. Oblikujmo izrek o potreben pogoj obstoj ekstrema.
Izrek.Če funkcija ƒ (X) na točki X 0 ima ekstrem, potem je odvod funkcije na tej točki enak nič, tj. ƒ¢ ( X 0)=0.
Naj takoj opozorimo, da ta pogoj ni zadosten, tj. obratna izjava ni vedno resnična. Iz enakosti ƒ ¢ ( X 0)= 0 ne sledi nujno temu v točki X 0 obstaja ekstrem.
To potrjuje primer s funkcijo ƒ (X)=x 3 .
Bomo našli ƒ ¢ ( X)= 3X 2 . Na točki X=0 ƒ ¢ (0)=0 . Ampak čim bližje bistvu, kot želite X=0 bomo našli X> 0, kjer ƒ (X)=x 3 > 0, bomo našli X< 0, где ¦ (X)=X 3 < 0. Т. е. не существует какая-либо малая окрестность точки X=0, kjer za vse X vrednost funkcije v točki X=0 bo največji ali najmanjši. Zato točka X=0 ni ekstremna točka.
Lahko se trdi drugače. Ker je izpeljanka ƒ ¢ (x)=3x 2 , nato funkcijo ƒ(x)=x 3 narašča za vsak realni x in nima ekstremov.
Točke, v katerih je izpolnjen nujni ekstremni pogoj (ƒ ¢ (x)=0) se imenujejo kritično .
Očitno je tangenta na graf funkcije v točkah, kjer je ƒ ¢ (x)=0, vzporedno z osjo x Ox .
Zadosten pogoj ekstrem je podan v naslednjih izrekih.
1. izrek.če X 0 je kritična točka funkcije in pri prehodu skozi njo odvod spremeni predznak X 0 je točka ekstrema, in sicer če odvod spremeni predznak iz plusa v minus, je točka maksimuma, če spremeni predznak iz minusa v plus, pa je točka minimuma.
Upoštevajte, da v točki ni ekstrema, če izpeljanka ne spremeni predznaka. Pravilo za preučevanje ekstrema z uporabo prvega odvoda je znano iz šolskega tečaja. Včasih je primerneje oblikovati zadosten pogoj za ekstrem z uporabo drugega odvoda.
Naj funkcija ƒ( X) je dvakrat diferencibilna v neki domeni (tj. ƒ( X) ima ƒ¢ ( X) In ƒ ¢¢ ( X)).
2. izrek.če X 0 – kritična točka funkcije ƒ(x) in ƒ ¢¢ (X 0 ) > 0 , To X 0 – najmanjša točka, če ƒ ¢¢ (X 0 ) < 0, то X 0 – največja točka.
Z uporabo drugega odvoda se določi konveksnost ali konkavnost grafa funkcije.
Konveksnost, konkavnost. Prevojna točka.
Krivulja y=ƒ(X) je poklican konveksnoth spodaj katera koli od nje tangenta
ƒ ¢¢ ( X) < 0.
Krivulja y=ƒ(X) je poklican konkavno na intervalu, če ležijo vse točke krivulje višje katera koli od nje tangenta v tem intervalu. Nato na tem intervalu
ƒ ¢¢(x) > 0
Opredelitev. Prevojna točka krivulja je točka, kjer je krivulja na eni strani konveksna, na drugi pa konkavna.
Na prelomni točki ƒ ¢¢ ( X)=0.
Torej, znak drugega odvoda (kot tudi znak same funkcije in njenega prvega odvoda) označuje značilnosti grafa funkcije. Poglejmo jih še enkrat.
Če za vse X na intervalu ( A, b) ƒ (X) > 0 (ƒ (X) < 0), potem graf leži nad (pod) osjo x.
Če za vse X na intervalu ( A, b) ƒ ¢ ( X) > 0 (ƒ ¢ ( X) < 0), то функция на (A, b) poveča (zmanjša).
Če za vse X na intervalu ( A, b) ƒ ¢¢ ( X) > 0 (ƒ ¢¢ ( X) < 0), то график на (A, b) konkavno (konveksno).
Enačba ƒ( X)=0 določa "ničle" funkcije, tj. točke presečišča grafa z osjo Ox.
Enačba ƒ ¢ ( X)=0 določa kritične točke.
Enačba ƒ ¢¢ ( X)=0 določa možne prevojne točke.
Shema študije funkcij
Za študij funkcije ƒ (X) in risanje y=ƒ(X) je treba najti:
1) domena definicije funkcije in presečišče grafa s koordinatnimi osemi;
2) intervali monotonije;
3) točke ekstremov in vrednosti funkcij na teh točkah;
4) intervali konveksnosti in konkavnosti grafa;
5) prevojne točke grafa;
6) v kartezičnem koordinatnem sistemu zgradite vse dobljene točke (včasih za razjasnitev grafa pridobite dodatne točke) in sam graf.
Najmanjša in največja vrednost funkcije na segmentu
Pri reševanju nekaterih problemov optimizacijske metode je pomembno, da lahko najdemo najmanjše ali največje vrednosti funkcije na določenem segmentu. Funkcija doseže te vrednosti na kritičnih točkah ali na koncih segmenta.
Shema iskanja najmanjšo in največjo vrednost funkcije ƒ (X) na segmentu [ A, b].
1. Poiščite odvod funkcije ƒ ¢ ( X).
2. Iz enačbe poiščite kritične točke ƒ ¢ ( X)=0.
3. Izberite kritične točke, ki pripadajo temu segmentu [ A, b] in poiščite vrednost funkcije ƒ (X) na vsaki takšni točki.
4. Izračunajte vrednosti funkcij ƒ (X) na koncih segmenta: ƒ( A) in ƒ( b).
5. Med dobljenimi vrednostmi funkcije izberi največjo (največja) in najmanjša (najmanjša).
Primer 2.
Poiščite največjo in najmanjšo vrednost funkcije ƒ(x)=X 3 –9x 2 +24h–10 na segmentu.
1. ƒ ¢ ( X)= 3X 2 – 9·2 X 2 + 24.
2. ƒ ¢ ( X)=0, 3(X 2 –6X+8)=0, X 1 =2, X 2 =4.
3. Točka x 2 =4 ne pripada odseku. Zato izračunamo vrednost funkcije le v točki X 1 =2
ƒ(2)=2 3 –9·2 2 +24·2–10=10.
4. Funkcijske vrednosti na koncih segmenta: ƒ(0)= –10, ƒ(3)=3 3 –9·3 2 +24·3–10, ƒ(3)=8.
5. Dobljene vrednosti:
ƒ(2)=10, ƒ(0)= –10, ƒ(3)=8.
Najvišja vrednost je 10 in je dosežena na točki X=2. Najmanjša je enaka –10 in je dosežena v točki X=0.
Primer 3.
Poiščite intervale konveksnosti in konkavnosti ter prevojne točke krivulje y=x+36X 2 –2X 3 –X 4 .
Domena definicije te funkcije je množica vseh realnih števil, tj. XЄ(–∞, +∞).
Poiščimo drugo izpeljanko.
pri¢ =1+72 X–6X 2 –4X 3 .
pri¢¢ =72–12 X–12X 2 = –12(X 2 +X–6).
Iz enačbe pri¢¢ =0 dobimo absciso prevojne točke:
–12(X 2 +X–6)=0 X 1 = –3; X 2 =2.
Določimo znak pri¢¢ v intervalih
(–∞; –3), (–3; 2), (2, +∞).
X
(–∞, –3)
(–3; 2)
(2; +∞)
pri¢¢
oblika krivulje
konveksen
pregib
konkavno
pregib
konveksen
Poiščimo ordinate prevojnih točk:
pri(–3)=726; M 1 (–3; 726) – prelomna točka
pri(2)=114; M 2 (2; 114) – prelomna točka.
Na intervalu (–3; 2) je krivulja konkavna. Na intervalih (–∞; –3) in (2; +∞) – konveksno.
Vzorci nalog
Naloga št. 1.
Poiščite prelomne točke funkcije in narišite graf

funkcija ƒ (X) je definiran za vse realne X in je zvezen na vsakem od navedenih intervalov: (–∞; –1), [–1; 0], (0, +∞). Raziščimo funkcijo ƒ (X) za kontinuiteto v točkah X= –1 in X=0.
Da bi to naredili, bomo na vsaki od teh točk našli enostranske meje.

Ker so enostranske meje drugačne, torej X = –1 – točka diskontinuitete prve vrste.

Enostranski limiti sta enaki, tj. v točki x=0 je limita funkcije in 
Primerjajmo to mejo z vrednostjo funkcije v točki: 
Ker  potem noter pri x=0 je funkcija ƒ(x) zvezna.
potem noter pri x=0 je funkcija ƒ(x) zvezna.
Narišimo funkcijo ƒ (X), glede na to
1)  – enačba premice,
– enačba premice,
2)  – enačba zgornjega polkroga
– enačba zgornjega polkroga  s središčem v izhodišču in polmerom, enakim enoti, in pod pogojem –1 £ X enačba £ 0
s središčem v izhodišču in polmerom, enakim enoti, in pod pogojem –1 £ X enačba £ 0  definira četrt kroga.
definira četrt kroga.
3) za X > 0 je graf podan z enačbo  . Presečišča te krivulje z osjo Ox najdemo iz enačbe
. Presečišča te krivulje z osjo Ox najdemo iz enačbe  za x > 0. x= π
n, Kje n
=1, 2, 3, 4,
za x > 0. x= π
n, Kje n
=1, 2, 3, 4,

riž. 2.
Naloga št. 2.
Napišite enačbe za tangente na premico  na točkah, kjer X=0 in X=4. Poiščite presečišče tangent in kot med njima. Narišite risbo.
na točkah, kjer X=0 in X=4. Poiščite presečišče tangent in kot med njima. Narišite risbo.
Enačba tangente na premico y=ƒ(x) izgleda kot
Kje pri 0 =ƒ( X 0).
Na točki X=0 pri(0)=ƒ(0)=5.
pri¢ =ƒ ¢ (X)=X–3 ƒ¢ (0)= –3.
M 1 (0, 5) ima obliko y– 5= –3(X–0) oz
y= –3X+5.
Na točki X=4 pri(4)=ƒ(4)=1. ƒ¢ (4)=4–3=1.
Enačba tangente v točki M 2 (4, 1) ima obliko y– 1=X–4 oz
y=x–3.
Z reševanjem sistema dobimo presečišče tangent

Presečišče M 3 (2, –1).
Kotiček φ med tangentami najdemo iz formule:
 ,
,
Kje k 1 = –3; k 2 =1 – kotni koeficienti tangent.
 .
.
Kotiček φ =arctg 2.
Zgradimo to linijo  – parabola z vrhom v točki, kjer X=3, ker pri¢
=0 pri X=3. Bomo našli
– parabola z vrhom v točki, kjer X=3, ker pri¢
=0 pri X=3. Bomo našli  . Pika M 4 (3;
. Pika M 4 (3;  ) je vrh parabole.
) je vrh parabole.
R 
je. 3.
Naloga št. 3.
Funkcija raziskovanja 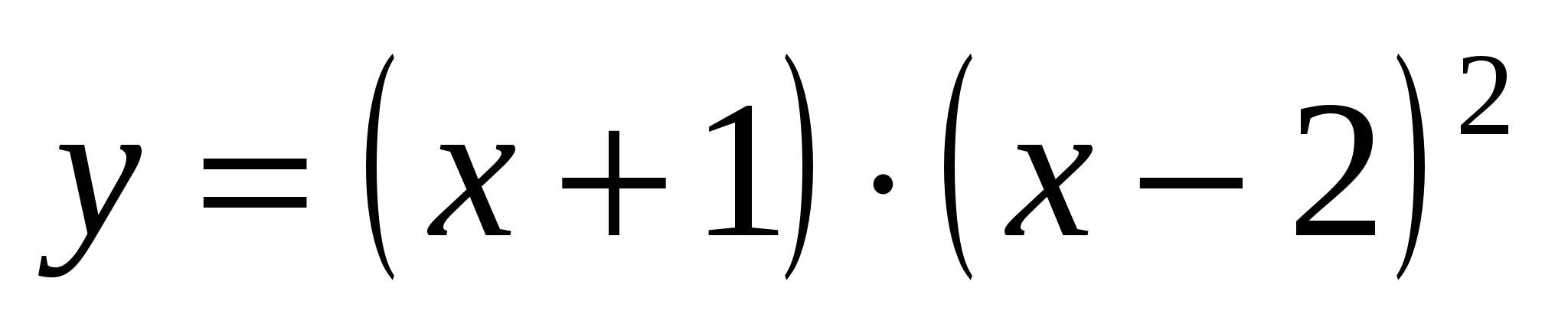 in ga začrtaj.
in ga začrtaj.
1. Ta funkcija je polinom (lahko odprete oklepaje, dobimo polinom tretje stopnje), zato je definirana, zvezna in diferenciabilna za poljubno X.
2. Poiščimo izpeljanko.
 .
.
Iz enačbe pri¢ =0 poiščemo kritične točke: 3 X·( X–2)=0, X 1 =0, X 2 =2.
Raziščimo jih.
X
(–∞, 0)
(0; 2)
(2; +∞)
pri ¢
pri
3. Torej funkcija narašča na intervalih (–∞, 0) in (2, +∞), pada na intervalu (0; 2), ima maksimum pri x=0 in minimum pri x=2:
pri max = pri(0)=4; pri min = pri(2)=0.
4. Poiščimo drugi odvod.
pri¢¢ = 6·( X-1).
Krivulja je konveksna, kjer pri¢¢ < 0, т. е. 6·(X–1) < 0, X < 1.
Krivulja je konkavna, kjer pri¢¢ > 0, tj. X > 1.
Torej, na intervalu (–∞, 1) je krivulja konveksna; in na intervalu (1, +∞) je konkaven.
5. Iz enačbe poiščemo prelomno točko pri¢¢ =0. torej X=1 – abscisa prevojne točke, ker ta točka ločuje intervale konveksnosti in konkavnosti krivulje. Ordinata prevojne točke: pri(1)=2.
Graf funkcije pri=(X+1)·( X–2) 2 seka os Ox pri pri=0, tj. ko X= –1 in X=2;
prečka os Oy pri X=0, tj. ko pri=4. Osvojili smo tri točke: (–1; 0), (2; 0), (0; 4). Vse dobljene točke bomo vnesli v tabelo in prišteli še tiste, ki so ob njih.
–2
–1



–16


je. 4 Krivulja y=(x+1)(x–2) 2.
Naloga št. 1
Predstavljamo vam naloge, ki imajo lahko enega, dva, tri ali več pravilnih odgovorov. Obkroži številke vseh pravilnih odgovorov.
1. Če  potem funkcija
potem funkcija
1) narašča
2) zmanjševanje
3) konstantna
2. Če
1) Povečanje
2) Zmanjševanje
3. Če  , nato funkcijo
, nato funkcijo
1) Povečanje
2) Zmanjševanje
4. Če  , nato funkcijo
, nato funkcijo
1) Naraščajoča 3) Zmanjšanje
2) Konstantno 4) Monotono
5. Funkcija  je
je
1) Celo
2) Niti ne
3) niti sodo niti liho
4) Periodično
5) Ne periodično
6) Trigonometrični
7) Osnovno
6. Funkcija  je
je
1) celo
2) liho
3) niti sodo niti liho
4) periodično
5) ni periodično
6) trigonometrični
7) osnovno
2) Weierstrass 4) Dirichlet 6) Leibniz
8) Rešitev  Enačbe
Enačbe
1) 0 3) 0 in 3 5) 2 7) 3
2) 2 in 3 4) 2 6) -5 in 1 8) 5 in 1
9) rešitev neenačbe 
1) ( ; 1) 3) (
; 1) 3) ( ; 1) 5) (-
; 1) 5) (- ;1)
;1)
2) (1; 5) 4) (2;  ) 6)
) 6) 
10) Metoda  Znesek je najden
Znesek je najden
1) vektorji
2) naravnost
3) segment
11) Če  , nato funkcijo
, nato funkcijo
1) Konkavno 3) Konveksno 5) Padajoče
2) Monotoni 4) Naraščajoči 6) Konstantni
12) domena definicije funkcije je enaka 
1) ( ;0)
;0)
2) (0;  )
)
3) (- ;
; )
)
4) (0;1)
5) 
6) 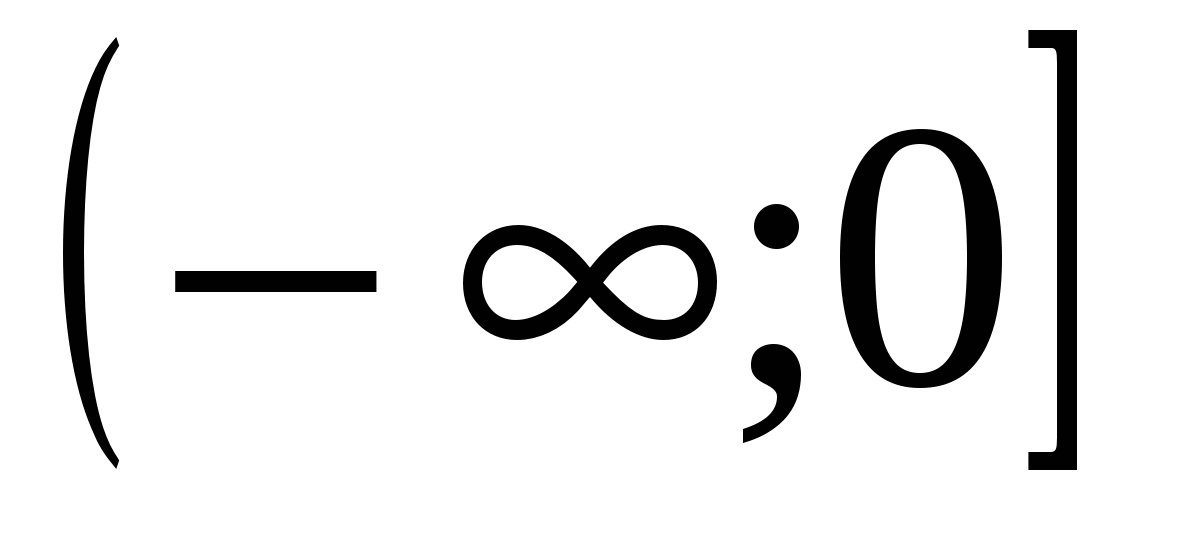
7) (-1;1)
8) 
9) 
13) funkcija  je
je
1) okvirno
2) trigonometrična
3) moč
4) logaritemski
14) če so funkcije y = x  potem je
potem je 
1) celo
2) liho
3) niti sodo niti liho
15) funkcija  pri
pri  je
je
Cilji lekcije:
Poučna- poznajo formule za diferenciacijo; pravila razlikovanja;
diferenciacija kompleksne funkcije; fizikalni in geometrijski pomen odvoda;
enačba tangente na graf funkcije.
Razvojni - znati najti odvode funkcij; reševanje problemov z uporabo fizičnega pomena, geometrijskega pomena; poiščejo vrednost odvoda funkcije v točki; matematično pravilno pojasniti in utemeljiti izvedena dejanja.
Izobraževalni – gojiti samostojnost, odgovornost, refleksijo.
Med poukom
I. Organizacijski trenutek.
II. Preverjanje domače naloge
(med odmori izvajalci preverjajo (učence) in ocenjujejo).
III. Postavljanje ciljev in motivacija
Učitelj učence obvesti, da je ta učna ura zadnja učna ura na temo »Izračunavanje odvodov« in jih povabi, da sami oblikujejo svoje cilje.
Učitelj: »Veliki filozof Konfucij je nekoč rekel: »Tri poti vodijo do znanja: pot razmišljanja je najplemenitejša pot, pot posnemanja je najlažja pot in pot izkušenj je najbolj grenka pot.« Tako bo danes pri pouku vsak od vas ugotovil, na kateri poti do znanja o tej temi je.«
Učenci dobijo nalogo, da pokažejo svoje znanje in spretnosti pri računanju odvodov in dobijo učni načrt.
stopnja I: Izpolnite nalogo s kartico »Zapomni si«.
(preverjanje poznavanja formul in pravil razlikovanja).
Stopnja II: Ustno frontalno delo pri ponavljanju in posploševanju znanja.
Faza III:"Testna napoved" (pri izvajanju te naloge je sprejemljiva pomoč svetovalcev).
jazStopnja V: Rešitev praktičnega problema.
Stopnja V: Samostojno delo
Ocenjuje se stopnja I, III, V dela in domače naloge. Svetovalci preverijo in rezultate vnesejo v ocenjevalno tabelo.
Kriteriji ocenjevanja: "5"- 19-20 točk;
"4"- 15-18 točk;
"3"- 10-14 točk.
Poti do znanja
- Reprodukcija in popravljanje referenčnega znanja
stopnja I.
Cilj: kontrola, samokontrola poznavanja formul in pravil razlikovanja
Ne pozabite! F.I. ___________________________________________________ |
|
Izpeljanka |
|
c,c - slabosti t |
|
|
|
|
|
f"(x)+ g"(x) |
|
f(x)* g(x) |
|
|
|
Na koncu te naloge se izvede samotestiranje z uporabo "Tabele izpeljank". Kartice se predajo v overitev svetovalcem (popravki na kartah niso dovoljeni).
V. Posploševanje in sistematizacija znanja
Stopnja II.
1. Ustno frontalno delo.
A. Ustvarite nalogo za ta pogoj in jo rešite.
![]()
1. Poiščite vrednost odvoda funkcije v točki t = 3. (Odgovor: 21.)
2. Sestavite enačbo za tangento na graf funkcije v točki t = 3. (Odgovor: y = 21x-45.).
3. Poiščite hitrost telesa in pospešek v trenutku t=3c, če je zakon gibanja podan s formulo. (Odgovor: 21 m/s, 16 m/s²).
4. Poiščite kotni koeficient tangente, narisane na graf funkcije v točki t = 3. (Odgovor: 21.).
5. Poiščite tangens naklonskega kota tangente na graf funkcije v točki t = 3 in določite vrsto kota med tangento in pozitivno smerjo osi Ox. (Odgovor: tgα, kot α je oster)
B. Poiščite odvode funkcij

2. Stopnja III"Testna napoved"


Na koncu te naloge se na podlagi končnih odgovorov izvede samotestiranje in se testi predajo svetovalcem. (popravki na kartah niso dovoljeni).
odgovori:
1 možnost |
||||
Možnost 2 |
- Rešitev problema
jazStopnja V
Frontalna rešitev naloge višje stopnje (rešitev izvajajo svetovalni delavci skupaj z razredom).
Naloga
Pri katerih vrednostih parametrov a tangente na graf funkcije ![]()
narisana v točkah njenega presečišča z osjo X, tvorita med seboj kot 60°?

Graf je parabola z vejami navzgor, ki sekajo os X v dveh točkah (primer a=0 ne ustreza pomenu problema):
IX. Seštevanje in ocenjevanje
1. Vprašanja: a) Ali je bil namen lekcije dosežen?
b) Katera stopnja se je zdela najtežja?
c) Kaj je bilo najbolj zanimivo?
2. Svetovalci objavijo rezultate (število in imena študentov na poti
posnemanje, načini refleksije in načini izkustva).

 .
.