A continuous random variable is given by the distribution density examples. Mathematics and computer science
9. Continuous random variable, its numerical characteristics
A continuous random variable can be specified using two functions. Integral probability distribution function of random variable X is called a function defined by the equality  .
.
The integral function gives general method assignments of both discrete and continuous random variables. In the case of a continuous random variable. All events: have the same probability, equal to the increment of the integral function on this interval, i.e.. For example, for the discrete random variable specified in example 26, we have:

Thus, the graph of the integral function of the function under consideration is a union of two rays and three segments parallel to the Ox axis.
Example 27. Continuous random variable X is specified by the integral probability distribution function
 .
.
Construct a graph of the integral function and find the probability that, as a result of the test, the random variable X will take a value in the interval (0.5;1.5).
Solution. On the interval  the graph is the straight line y = 0. In the interval from 0 to 2 there is a parabola, given by the equation
the graph is the straight line y = 0. In the interval from 0 to 2 there is a parabola, given by the equation  . On the interval
. On the interval  The graph is the straight line y = 1.
The graph is the straight line y = 1.
The probability that the random variable X as a result of the test will take a value in the interval (0.5;1.5) is found using the formula.
Thus, .
Properties of the integral probability distribution function:
It is convenient to specify the distribution law of a continuous random variable using another function, namely, probability density function .
.
The probability that the value assumed by the random variable X falls within the interval  , is determined by the equality
, is determined by the equality  .
.
The graph of a function is called distribution curve. Geometrically, the probability of a random variable X falling into the interval is equal to the area of the corresponding curvilinear trapezoid bounded by the distribution curve, the Ox axis and straight lines  .
.
Properties of the probability density function:

9.1. Numerical characteristics of continuous random variables
Expected value(average value) of a continuous random variable X is determined by the equality  .
.
M(X) is denoted by A. The mathematical expectation of a continuous random variable has properties similar to those of a discrete random variable:
Variance discrete random variable X is the mathematical expectation of the squared deviation of the random variable from its mathematical expectation, i.e. . For a continuous random variable, the variance is given by the formula  .
.
The dispersion has the following properties:

The last property is very convenient to use to find the variance of a continuous random variable.
The concept of standard deviation is introduced similarly. The standard deviation of the continuous random variable X is called the square root of the variance, i.e.  .
.
Example 28. A continuous random variable X is specified by a probability density function  in the interval (10;12), outside this interval the value of the function is 0. Find 1) the value of the parameter A, 2) mathematical expectation M(X), variance
in the interval (10;12), outside this interval the value of the function is 0. Find 1) the value of the parameter A, 2) mathematical expectation M(X), variance  , standard deviation, 3) integral function
, standard deviation, 3) integral function  and build graphs of integral and differential functions.
and build graphs of integral and differential functions.
1). To find a parameter A use the formula  . We'll get it. Thus,
. We'll get it. Thus,  .
.
2). To find the mathematical expectation, we use the formula: , from which it follows that  .
.
We will find the variance using the formula:  , i.e. .
, i.e. .
Let's find the standard deviation using the formula: , from which we get that  .
.
3). The integral function is expressed through the probability density function as follows:  . Hence,
. Hence,  at
at  , = 0 at
, = 0 at  u = 1 at
u = 1 at  .
.
The graphs of these functions are presented in Fig. 4. and fig. 5.
Fig.4 Fig.5.
9.2. Uniform probability distribution of a continuous random variable
Probability distribution of a continuous random variable X evenly on the interval if its probability density is constant on this interval and equal to zero outside this interval, i.e. . It is easy to show that in this case  .
.
If the interval  is contained in the interval, then
is contained in the interval, then  .
.
Example 29. An instantaneous signal event must occur between one o'clock and five o'clock. The signal waiting time is a random variable X. Find the probability that the signal will be detected between two and three o'clock in the afternoon.
Solution. Random value X has a uniform distribution, and using the formula we find that the probability that the signal will be between 2 and 3 o'clock in the afternoon is equal to  .
.
In educational and other literature it is often denoted in the literature through  .
.
9.3. Normal probability distribution of a continuous random variable
The probability distribution of a continuous random variable is called normal if its probability distribution law is determined by the probability density  . For such quantities A- expected value,
. For such quantities A- expected value,  - standard deviation.
- standard deviation.
Theorem. Probability of a normally distributed continuous random variable falling into a given interval  determined by the formula
determined by the formula  , Where
, Where  - Laplace function.
- Laplace function.
A consequence of this theorem is the three sigma rule, i.e. It is almost certain that a normally distributed, continuous random variable X takes its values in the interval  . This rule can be derived from the formula
. This rule can be derived from the formula  , which is a special case of the formulated theorem.
, which is a special case of the formulated theorem.
Example 30. The lifespan of the TV is a random variable X, subordinate normal law distribution, with a warranty period of 15 years and a standard deviation of 3 years. Find the probability that the TV will last from 10 to 20 years.
Solution. According to the conditions of the problem, the mathematical expectation A= 15, standard deviation.
Let's find . Thus, the probability of the TV operating from 10 to 20 years is more than 0.9.
9.4. Chebyshev's inequality
Occurs Chebyshev's lemma. If a random variable X takes only non-negative values and has a mathematical expectation, then for any positive V .
.
Considering that , as the sum of the probabilities of opposite events, we obtain that  .
.
Chebyshev's theorem. If the random variable X has finite variance  and mathematical expectation M(X), then for any positive
and mathematical expectation M(X), then for any positive  inequality is true
inequality is true .
.
Whence it follows that  .
.
Example 31. A batch of parts has been produced. The average length of the parts is 100 cm, and the standard deviation is 0.4 cm. Estimate below the probability that the length of a part taken at random will be at least 99 cm. and no more than 101cm.
Solution. Variance. The mathematical expectation is 100. Therefore, to estimate from below the probability of the event in question  let us apply Chebyshev's inequality, in which
let us apply Chebyshev's inequality, in which  , Then
, Then  .
.
10. Elements of mathematical statistics
Statistical aggregate name a set of homogeneous objects or phenomena. Number P elements of this set is called the volume of the collection. Observed values  trait X is called options. If the options are arranged in increasing sequence, then we get discrete variation series. In the case of grouping, the option by intervals turns out to be interval variation series. Under frequency t characteristic values understand the number of members of the population with a given variant.
trait X is called options. If the options are arranged in increasing sequence, then we get discrete variation series. In the case of grouping, the option by intervals turns out to be interval variation series. Under frequency t characteristic values understand the number of members of the population with a given variant.
The ratio of frequency to volume of a statistical population is called relative frequency sign:  .
.
The relationship between the variants of a variation series and their frequencies is called statistical distribution of the sample. A graphical representation of the statistical distribution can be polygon frequency
Example 32. By surveying 25 first-year students, the following data about their age was obtained:  . Compile a statistical distribution of students by age, find the range of variation, construct a frequency polygon and compile a series of distributions of relative frequencies.
. Compile a statistical distribution of students by age, find the range of variation, construct a frequency polygon and compile a series of distributions of relative frequencies.
Solution. Using the data obtained from the survey, we will create a statistical distribution of the sample
|
The range of the variation sample is 23 – 17 = 6. To construct a frequency polygon, construct points with coordinates  and connect them in series.
and connect them in series.
The relative frequency distribution series has the form:
|
10.1.Numerical characteristics of the variation series
Let the sample be given by a series of frequency distributions of feature X:
|
|
|
|
||
|
|
|
The sum of all frequencies is equal P.
Arithmetic mean of the sample name the quantity  .
.
Variance or the measure of dispersion of the values of a characteristic X in relation to its arithmetic mean is called the value  . The standard deviation is the square root of the variance, i.e. .
. The standard deviation is the square root of the variance, i.e. .
The ratio of the standard deviation to the arithmetic mean of the sample, expressed as a percentage, is called coefficient of variation: .
.
Empirical relative frequency distribution function call a function that determines for each value the relative frequency of an event  , i.e.
, i.e.  , Where
, Where  - number of options, smaller X, A P– sample size.
- number of options, smaller X, A P– sample size.
Example 33. Under the conditions of example 32, find the numerical characteristics  .
.
Solution. Let's find the arithmetic mean of the sample using the formula, then .
The variance of trait X is found by the formula: , i.e. . The standard deviation of the sample is  . The coefficient of variation is
. The coefficient of variation is  .
.
10.2. Probability estimation by relative frequency. Confidence interval
Let it be carried out P independent trials, in each of which the probability of occurrence of event A is constant and equal to R. In this case, the probability that the relative frequency will differ from the probability of the occurrence of event A in each trial in absolute value is no more than by approximately equal to twice the value of the Laplace integral function:  .
.
Interval estimation call such an estimate, which is determined by two numbers that are the ends of the interval covering the estimated parameter of the statistical population.
Confidence interval is an interval that, with a given confidence probability
is an interval that, with a given confidence probability  covers the estimated parameter of the statistical population. Considering the formula in which we replace the unknown quantity R to its approximate value
covers the estimated parameter of the statistical population. Considering the formula in which we replace the unknown quantity R to its approximate value  obtained from the sample data, we obtain:
obtained from the sample data, we obtain:  . This formula is used to estimate probability by relative frequency. Numbers
. This formula is used to estimate probability by relative frequency. Numbers  And
And  called lower and, respectively, upper trust boundaries, - the maximum error for a given confidence probability
called lower and, respectively, upper trust boundaries, - the maximum error for a given confidence probability  .
.
Example 34. The factory workshop produces light bulbs. When checking 625 lamps, 40 were found to be defective. Find, with a confidence probability of 0.95, the boundaries within which the percentage of defective light bulbs produced by the factory workshop lies.
Solution. According to the conditions of the task. We use the formula  . Using Table 2 of the appendix, we find the value of the argument, in which the value of the Laplace integral function is equal to 0.475. We get that
. Using Table 2 of the appendix, we find the value of the argument, in which the value of the Laplace integral function is equal to 0.475. We get that  . Thus, . Therefore, we can say with a probability of 0.95 that the share of defects produced by the workshop is high, namely, it varies from 6.2% to 6.6%.
. Thus, . Therefore, we can say with a probability of 0.95 that the share of defects produced by the workshop is high, namely, it varies from 6.2% to 6.6%.
10.3. Parameter Estimation in Statistics
Let the quantitative characteristic X of the entire population under study ( population) has a normal distribution.
If the standard deviation is known, then the confidence interval covering the mathematical expectation A 
 , Where P– sample size,
, Where P– sample size,  - sample arithmetic mean, t is the argument of the Laplace integral function, at which
- sample arithmetic mean, t is the argument of the Laplace integral function, at which  . Moreover, the number
. Moreover, the number  called estimation accuracy.
called estimation accuracy.
If the standard deviation is unknown, then from the sample data it is possible to construct a random variable that has a Student distribution with P– 1 degrees of freedom, which is determined by only one parameter P and does not depend on unknowns A And . Student's t-distribution even for small samples  gives quite satisfactory ratings. Then the confidence interval covering the mathematical expectation A of this feature with a given confidence probability is found from the condition
gives quite satisfactory ratings. Then the confidence interval covering the mathematical expectation A of this feature with a given confidence probability is found from the condition 
 , where S is the corrected root mean square,
, where S is the corrected root mean square,  - Student’s coefficient, found from the data
- Student’s coefficient, found from the data  from table 3 of the appendix.
from table 3 of the appendix.
The confidence interval covering the standard deviation of this characteristic with a confidence probability is found using the formulas: and , where  found from the table of values q
according to .
found from the table of values q
according to .
10.4. Statistical methods studying dependencies between random variables
The correlation dependence of Y on X is the functional dependence of the conditional average  from X. The equation
from X. The equation  represents the regression equation of Y on X, and
represents the regression equation of Y on X, and  - regression equation of X on Y.
- regression equation of X on Y.
The correlation dependence can be linear or curvilinear. In the case of a linear correlation dependence, the equation of the straight regression line has the form:  , where the slope A straight line of regression Y on X is called the sample regression coefficient Y on X and is denoted
, where the slope A straight line of regression Y on X is called the sample regression coefficient Y on X and is denoted  .
.
For small samples, the data is not grouped, the parameters  are found using the least squares method from the system of normal equations:
are found using the least squares method from the system of normal equations:
 , Where P– number of observations of values of pairs of interrelated quantities.
, Where P– number of observations of values of pairs of interrelated quantities.
Sample linear correlation coefficient  shows the close relationship between Y and X. The correlation coefficient is found using the formula
shows the close relationship between Y and X. The correlation coefficient is found using the formula  , and
, and  , namely:
, namely:

The sample equation of the straight regression line Y on X has the form:
 .
.
At large number observations of signs X and Y, a correlation table is compiled with two inputs, with the same value X observed  times, same meaning at observed
times, same meaning at observed  times, same pair
times, same pair  observed
observed  once.
once.
Example 35. A table of observations of signs X and Y is given.
|
Find the sample equation of the straight regression line Y on X.
Solution. The relationship between the studied characteristics can be expressed by the equation of a straight line of regression of Y on X: . To calculate the coefficients of the equation, let's create a calculation table:
Observation no. |
|
|
||
Concepts of mathematical expectation M(X) and variance D(X), introduced earlier for a discrete random variable, can be extended to continuous random variables.
· Mathematical expectation M(X) continuous random variable X is determined by the equality:
provided that this integral converges.
· Variance D(X) continuous random variable X is determined by the equality:
· Standard deviationσ( X) continuous random variable is determined by the equality:
All properties of mathematical expectation and dispersion, discussed earlier for discrete random variables, are also valid for continuous ones.
Problem 5.3. Random value X given by a differential function f(x):
Find M(X), D(X), σ( X), and P(1 < X< 5).
Solution:
M(X)= =
+ = 8/9 0+9/6 4/6=31/18,
D(X)=
= = /
P 1 =
Tasks
5.1. X
f(x), and
R(‒1/2 < X< 1/2).
5.2. Continuous random variable X given by the distribution function:
Find the differential distribution function f(x), and
R(2π /9< X< π /2).
5.3. Continuous random variable X
Find: a) number With; b) M(X), D(X).
5.4. Continuous random variable X given by the distribution density:
Find: a) number With; b) M(X), D(X).
5.5. X:
Find: a) F(X) and build its graph; b) M(X), D(X), σ( X); c) the probability that in four independent trials the value X will take exactly 2 times the value belonging to the interval (1;4).
5.6. The probability distribution density of a continuous random variable is given X:
Find: a) F(X) and build its graph; b) M(X), D(X), σ( X); c) the probability that in three independent trials the value X will take exactly 2 times the value belonging to the segment .
5.7. Function f(X) is given in the form:
With X; b) distribution function F(x).
5.8. Function f(x) is given in the form:
Find: a) the value of the constant With, at which the function will be the probability density of some random variable X; b) distribution function F(x).
5.9. Random value X, concentrated on the interval (3;7), is specified by the distribution function F(X)= X will take the value: a) less than 5, b) not less than 7.
5.10. Random value X, centered on the interval (-1;4), is specified by the distribution function F(X)= . Find the probability that the random variable X will take the value: a) less than 2, b) less than 4.
5.11.
Find: a) number With; b) M(X); c) probability R(X > M(X)).
5.12. The random variable is specified by the differential distribution function:
Find: a) M(X); b) probability R(X ≤ M(X)).
5.13. The Rem distribution is given by the probability density:
Prove that f(x) is indeed a probability density function.
5.14. The probability distribution density of a continuous random variable is given X:
Find the number With.
5.15. Random value X distributed according to Simpson's law ( isosceles triangle) on the segment [-2;2] (Fig. 5.4). Find an analytical expression for the probability density f(x) on the entire number line.
Rice. 5.4 Fig. 5.5
5.16. Random value X distributed according to law" right triangle" in the interval (0;4) (Fig. 5.5). Find an analytical expression for the probability density f(x) on the entire number line.
Answers
P (-1/2<X<1/2)=2/3.
P(2π /9<X< π /2)=1/2.
5.3. A) With=1/6, b) M(X)=3 , c) D(X)=26/81.
5.4. A) With=3/2, b) M(X)=3/5, c) D(X)=12/175.
b) M(X)= 3 , D(X)= 2/9, σ( X)= /3.
b) M(X)=2 , D(X)= 3 , σ( X)= 1,893.
5.7. a) c = ; b)
5.8. A) With=1/2; b)
5.9. a)1/4; b) 0.
5.10. a)3/5; b) 1.
5.11. A) With= 2; b) M(X)= 2; in 1- ln 2 2 ≈ 0,5185.
5.12. A) M(X)= π /2; b) 1/2
Chapter 6. Continuous random variables.
§ 1. Density and distribution function of a continuous random variable.
The set of values of a continuous random variable is uncountable and usually represents some finite or infinite interval.
A random variable x(w) defined in a probability space (W, S, P) is called continuous(absolutely continuous) W, if there is a non-negative function such that for any x the distribution function Fx(x) can be represented as an integral
The function is called a function probability distribution densities.
The definition implies the properties of the distribution density function:
1..gif" width="97" height="51">
3. At points of continuity, the distribution density is equal to the derivative of the distribution function: .
4. The distribution density determines the law of distribution of a random variable, since it determines the probability of a random variable falling into the interval:
5. The probability that a continuous random variable will take a specific value is zero: . Therefore, the following equalities are valid:
The graph of the distribution density function is called distribution curve, and the area bounded by the distribution curve and the x-axis is equal to unity. Then, geometrically, the value of the distribution function Fx(x) at point x0 is the area bounded by the distribution curve and the x-axis and lying to the left of point x0.
Task 1. The density function of a continuous random variable has the form:
![]()
Determine the constant C, construct the distribution function Fx(x) and calculate the probability.
Solution. The constant C is found from the condition We have:
 whence C=3/8.
whence C=3/8.
To construct the distribution function Fx(x), note that the interval divides the range of values of the argument x (numeric axis) into three parts: https://pandia.ru/text/78/107/images/image017_17.gif" width="264 " height="49">
since the density x on the semi-axis is zero. In the second case
Finally, in the last case, when x>2,
Since the density vanishes on the semi-axis. So, the distribution function is obtained

Probability Let's calculate using the formula. Thus,
§ 2. Numerical characteristics of a continuous random variable
Expected value for continuously distributed random variables is determined by the formula https://pandia.ru/text/78/107/images/image028_11.gif" width="205" height="56 src=">,
if the integral on the right converges absolutely.
Dispersion x can be calculated using the formula  , and also, as in the discrete case, according to the formula https://pandia.ru/text/78/107/images/image031_11.gif" width="123" height="49 src=">.
, and also, as in the discrete case, according to the formula https://pandia.ru/text/78/107/images/image031_11.gif" width="123" height="49 src=">.
All properties of mathematical expectation and dispersion given in Chapter 5 for discrete random variables are also valid for continuous random variables.
Problem 2. For the random variable x from Problem 1, calculate the mathematical expectation and variance .
Solution.
And that means
https://pandia.ru/text/78/107/images/image035_9.gif" width="184" height="69 src=">
For a uniform distribution density graph, see Fig. .
Fig.6.2. Distribution function and distribution density. uniform law
The distribution function Fx(x) of a uniformly distributed random variable is equal to
Fx(x)= 
Expectation and variance; .
Exponential (exponential) distribution. A continuous random variable x taking non-negative values has an exponential distribution with parameter l>0 if the probability density distribution of the random variable is equal to
рx(x)= 
Rice. 6.3. Distribution function and distribution density of the exponential law.
The distribution function of the exponential distribution has the form
Fx(x)=https://pandia.ru/text/78/107/images/image041_8.gif" width="17" height="41">.gif" width="13" height="15"> and if its distribution density is equal to
 .
.
Through denotes the set of all random variables distributed according to a normal law with parameters parameters and .
The distribution function of a normally distributed random variable is equal to
 .
.
Rice. 6.4. Distribution function and normal distribution density
The parameters of the normal distribution are the mathematical expectation https://pandia.ru/text/78/107/images/image048_6.gif" width="64 height=24" height="24">
In the special case when https://pandia.ru/text/78/107/images/image050_6.gif" width="44" height="21 src="> normal distribution is called standard, and the class of such distributions is denoted by https://pandia.ru/text/78/107/images/image052_6.gif" width="119" height="49">,
and the distribution function

Such an integral cannot be calculated analytically (it is not taken in “quadratures”), and therefore tables have been compiled for the function. The function is related to the Laplace function introduced in Chapter 4
 ,
,
by the following relation ![]() . In the case of arbitrary parameter values https://pandia.ru/text/78/107/images/image043_5.gif" width="21" height="21 src="> the distribution function of a random variable is related to the Laplace function using the relation:
. In the case of arbitrary parameter values https://pandia.ru/text/78/107/images/image043_5.gif" width="21" height="21 src="> the distribution function of a random variable is related to the Laplace function using the relation:
![]() .
.
Therefore, the probability of a normally distributed random variable falling into an interval can be calculated using the formula
![]() .
.
A non-negative random variable x is called lognormally distributed if its logarithm h=lnx obeys the normal law. The expected value and variance of a lognormally distributed random variable are Mx= and Dx=.
Task 3. Let a random variable be given https://pandia.ru/text/78/107/images/image065_5.gif" width="81" height="23">.
Solution. Here https://pandia.ru/text/78/107/images/image068_5.gif" width="573" height="45">
Laplace distribution is given by the function fx(x)=https://pandia.ru/text/78/107/images/image070_5.gif" width="23" height="41"> and the kurtosis is gx=3.
Fig.6.5. Laplace distribution density function.
Random variable x is distributed over Weibull's law, if it has a distribution density function equal to https://pandia.ru/text/78/107/images/image072_5.gif" width="189" height="53">
The Weibull distribution governs the failure-free operation times of many technical devices. In problems of this profile, an important characteristic is the failure rate (mortality rate) l(t) of the studied elements of age t, determined by the relation l(t)=. If a=1, then the Weibull distribution turns into an exponential distribution, and if a=2 - into the so-called distribution Rayleigh.
Mathematical expectation of the Weibull distribution: -https://pandia.ru/text/78/107/images/image075_4.gif" width="219" height="45 src=">, where Г(а) is the Euler function. .
IN various tasks In applied statistics, so-called “truncated” distributions are often encountered. For example, tax authorities are interested in the distribution of income of those individuals whose annual income exceeds a certain threshold c0 established by tax laws. These distributions turn out to approximately coincide with the Pareto distribution. Pareto distribution given by functions
Fx(x)=P(x
Here https://pandia.ru/text/78/107/images/image081_4.gif" width="60" height="21 src=">.
Task 4. The random variable is uniformly distributed on the segment. Find the density of a random variable.
Solution. From the problem conditions it follows that

Next, the function is a monotone and differentiable function on an interval and has inverse function ![]() , whose derivative is equal to Therefore,
, whose derivative is equal to Therefore,

§ 5. Pair of continuous random variables
Let two continuous random variables x and h be given. Then the pair (x, h) defines a “random” point on the plane. The pair (x, h) is called random vector or two-dimensional random variable.
Joint distribution function random variables x and h and the function is called F(x, y)=Phttps://pandia.ru/text/78/107/images/image093_3.gif" width="173" height="25">. joint density probability distribution of random variables x and h is called a function such that ![]() .
.
The meaning of this definition of joint distribution density is as follows. The probability that a “random point” (x, h) will fall into a region on a plane is calculated as the volume of a three-dimensional figure – a “curvilinear” cylinder bounded by the surface https://pandia.ru/text/78/107/images/image098_3. gif" width="211" height="39 src=">
The simplest example of a joint distribution of two random variables is the two-dimensional uniform distribution on the setA. Let a bounded set M be given with area. It is defined as the distribution of the pair (x, h), defined by the following joint density:

Task 5. Let a two-dimensional random vector (x, h) be uniformly distributed inside the triangle. Calculate the probability of the inequality x>h.
Solution. The area of the indicated triangle is equal to (see Fig. No.?). By virtue of the definition of a two-dimensional uniform distribution, the joint density of random variables x, h is equal to

An event corresponds to a set ![]() on a plane, i.e. a half-plane. Then the probability
on a plane, i.e. a half-plane. Then the probability
On the half-plane B, the joint density is zero outside the set https://pandia.ru/text/78/107/images/image102_2.gif" width="15" height="17">. Thus, the half-plane B is divided into two sets and https://pandia.ru/text/78/107/images/image110_1.gif" width="17" height="23"> and , and the second integral is equal to zero, since the joint density there is equal to zero. That's why
If the joint distribution density for a pair (x, h) is given, then the densities of both components x and h are called private densities and are calculated using the formulas:
https://pandia.ru/text/78/107/images/image116_1.gif" width="224" height="23 src=">
For continuously distributed random variables with densities рx(х), рh(у), independence means that
Task 6. In the conditions of the previous problem, determine whether the components of the random vector x and h are independent?
Solution. Let us calculate the partial densities and . We have:
https://pandia.ru/text/78/107/images/image119_1.gif" width="283" height="61 src=">
Obviously, in our case https://pandia.ru/text/78/107/images/image121_1.gif" width="64" height="25"> is the joint density of the quantities x and h, and j(x, y) is a function of two arguments, then
https://pandia.ru/text/78/107/images/image123_1.gif" width="184" height="152 src=">
Task 7. In the conditions of the previous problem, calculate .
Solution. According to the above formula we have:
![]() .
.
Representing the triangle as
https://pandia.ru/text/78/107/images/image127_1.gif" width="479" height="59">
§ 5. Density of the sum of two continuous random variables
Let x and h be independent random variables with densities https://pandia.ru/text/78/107/images/image128_1.gif" width="43" height="25">. The density of the random variable x + h is calculated by formula convolution
https://pandia.ru/text/78/107/images/image130_0.gif" width="39" height="19 src=">. Calculate the density of the sum.
Solution. Since x and h are distributed according to the exponential law with the parameter , their densities are equal

Hence,
https://pandia.ru/text/78/107/images/image134_0.gif" width="339 height=51" height="51">
If x<0, то в этой формуле аргумент https://pandia.ru/text/78/107/images/image136_0.gif" width="65" height="25">is negative, and therefore . Therefore, if https://pandia.ru/text/78/107/images/image140_0.gif" width="359 height=101" height="101">
Thus we got the answer:
https://pandia.ru/text/78/107/images/image142_0.gif" width="40" height="41 "> is normally distributed with parameters 0 and 1. Random variables x1 and x2 are independent and have normal distributions with parameters a1, and a2, respectively. Prove that x1 + x2 has a normal distribution. The random variables x1, x2, ... xn are distributed and independent and have the same distribution density function.
 .
.
Find the distribution function and density of distribution of values:
a) h1 = min (x1, x2, ...xn) ; b) h(2) = max (x1,x2, ... xn)
Random variables x1, x2, ... xn are independent and uniformly distributed on the interval [a, b]. Find distribution functions and density functions of distributions of quantities
x(1) = min (x1,x2, ... xn) and x(2)= max(x1, x2, ...xn).
Prove that Mhttps://pandia.ru/text/78/107/images/image147_0.gif" width="176" height="47">.
The random variable is distributed according to Cauchy's law Find: a) coefficient a; b) distribution function; c) the probability of falling into the interval (-1, 1). Show that the mathematical expectation of x does not exist. The random variable is subject to Laplace's law with the parameter l (l>0): Find the coefficient a; construct distribution density graphs and distribution functions; find Mx and Dx; find the probabilities of events (|x|< и {çxç<}. Случайная величина x подчинена закону Симпсона на отрезке [-а, а], т. е. график её плотности распределения имеет вид:
Write a formula for the distribution density, find Mx and Dx.
Computational tasks.
A random point A has a uniform distribution in a circle of radius R. Find the mathematical expectation and variance of the distance r of the point to the center of the circle. Show that the value r2 is uniformly distributed on the segment. ![]()
The distribution density of a random variable has the form: 
Calculate the constant C, the distribution function F(x), and the probability ![]() The distribution density of a random variable has the form:
The distribution density of a random variable has the form: 
Calculate the constant C, the distribution function F(x), and the probability ![]() The distribution density of a random variable has the form:
The distribution density of a random variable has the form: 
Calculate the constant C, the distribution function F(x), , variance and probability. A random variable has a distribution function 
Calculate the density of a random variable, mathematical expectation, variance and probability Check that the function = 
may be a distribution function of a random variable. Find the numerical characteristics of this quantity: Mx and Dx. The random variable is uniformly distributed on the segment. Write down the distribution density. Find the distribution function. Find the probability of a random variable falling on the segment and on the segment. The distribution density x is equal to
 .
.
Find the constant c, the distribution density h = and the probability
P (0.25 The failure-free operation time of a computer is distributed according to an exponential law with the parameter l = 0.05 (failures per hour), i.e., it has a density function p(x) = Solving a certain problem requires trouble-free operation of the machine for 15 minutes. If a failure occurs while solving a problem, the error is detected only after the solution is completed, and the problem is solved again. Find: a) the probability that during the solution of the problem not a single failure will occur; b) the average time in which the problem will be solved. A rod 24 cm long is broken into two parts; We will assume that the break point is distributed evenly along the entire length of the rod. What is the average length of most of the rod? A piece of length 12 cm is randomly cut into two parts. The cut point is evenly distributed along the entire length of the segment. What is the average length of the small part of the segment? The random variable is uniformly distributed on the segment. Find the distribution density of the random variable a) h1 = 2x + 1; b) h2 =-ln(1-x); c) h3 = . Show that if x has a continuous distribution function F(x) = P(x Find the density function and distribution function of the sum of two independent quantities x and h with uniform distribution laws on the segments and, respectively. The random variables x and h are independent and uniformly distributed on the segments and, respectively. Calculate the density of the sum x+h. The random variables x and h are independent and uniformly distributed on the segments and, respectively. Calculate the density of the sum x+h. The random variables x and h are independent and uniformly distributed on the segments and, respectively. Calculate the density of the sum x+h. Random variables are independent and have an exponential distribution with density Continuous random variables - These are quantities whose possible values form a certain finite or infinite interval. The cumulative distribution function is the distribution law of a random variable, with the help of which you can specify both a discrete and a continuous random variable. Cumulative distribution function is called a function F(x), which determines for each value x the probability that the random variable X will take a value less than x, i.e. . Geometrically, this means: F(x) is the probability that the random variable X will take the value that is represented on the number axis by a point lying to the left of point x. Random value is called continuous if its integral function F(X) is continuously differentiable. Properties of the integral function. 10 . The values of the integral function belong to the segment from 0 to 1, that is. 20 . The integral function is a non-decreasing function, that is, if , then Consequences: 1. The probability that the SV will take the value contained in the interval (a; b) is equal to the increment of the integral function on this interval: 2. The probability that the NSV will take one specific value is 0. 3. If the possible values of the NSV are located along the entire number line, then the following limit relations are valid: Integral function graph. The graph of the integral function is constructed based on its properties. According to the first property, the graph is located between the straight lines y=0 and y=1. from the second property it follows that - is an increasing function, which means its graph on the interval (a, b) rises to the right and up. By 3 0 property at Figure 5. Graph of the integral function. Example 31. DSV is given by the distribution law Find the cumulative distribution function and plot its graph. 1. If , then 3 0 each. 2. If , . 3. If , . 4. If , then 3 0 each. Let's plot the integral function DSV(CH) (Fig. 6). Figure 6. Graph of the integral function for a discrete random variable. Differential distribution function of NSV. There is another way to specify the NSV using the differential distribution function. Differential The distribution function is a function equal to the first derivative of the integral function, that is. The differential distribution function is also called the probability density function. Theorem 17. The probability that NSV X will take a value belonging to the interval (a, b) is equal to a certain integral of the differential function, taken in the range from a to b. Example 32. The NSV is specified by the cumulative distribution function Find the differential distribution function and the probability of the NSV falling into the interval. Solution. Properties of the differential distribution function. 10 . A differential function is a non-negative function: . 20 . (Normalization condition.) The improper integral of the differential function in the range from -∞ to +∞ is equal to 1, that is: In particular, if all possible values of the NSV belong to the interval (a, b), then Example 33. Find parameter value A. Note that knowing the differential distribution function, you can find the integral function using the formula: Example 34. The NSV is specified by the differential distribution function: find the cumulative distribution function. Solution. 1. 3. Numerical characteristics of NSV. Random variable
is a variable that can take on certain values depending on various circumstances, and random variable is called continuous
, if it can take any value from any limited or unlimited interval. For a continuous random variable, it is impossible to indicate all possible values, so we designate intervals of these values that are associated with certain probabilities. Examples of continuous random variables include: the diameter of a part being ground to a given size, the height of a person, the flight range of a projectile, etc. Since for continuous random variables the function F(x), Unlike discrete random variables, has no jumps anywhere, then the probability of any individual value of a continuous random variable is zero. This means that for a continuous random variable it makes no sense to talk about the probability distribution between its values: each of them has zero probability. However, in a sense, among the values of a continuous random variable there are “more and less probable”. For example, hardly anyone would doubt that the value of a random variable - the height of a randomly encountered person - 170 cm - is more likely than 220 cm, although both values can occur in practice. As a distribution law that makes sense only for continuous random variables, the concept of distribution density or probability density is introduced. Let's approach it by comparing the meaning of the distribution function for a continuous random variable and for a discrete random variable. So, the distribution function of a random variable (both discrete and continuous) or integral function is called a function that determines the probability that the value of a random variable X less than or equal to the limit value X. For a discrete random variable at the points of its values x1
, x 2
, ..., x i,... masses of probabilities are concentrated p1
, p 2
, ..., p i,..., and the sum of all masses is equal to 1. Let us transfer this interpretation to the case of a continuous random variable. Let's imagine that a mass equal to 1 is not concentrated at individual points, but is continuously “smeared” along the abscissa axis Oh with some uneven density. Probability of a random variable falling into any area Δ x will be interpreted as the mass per section, and the average density at that section as the ratio of mass to length. We have just introduced an important concept in probability theory: distribution density. Probability density f(x) of a continuous random variable is the derivative of its distribution function: Knowing the density function, you can find the probability that the value of a continuous random variable belongs to the closed interval [ a; b]: the probability that a continuous random variable X will take any value from the interval [ a; b], is equal to a certain integral of its probability density ranging from a before b: In this case, the general formula of the function F(x) probability distribution of a continuous random variable, which can be used if the density function is known f(x)
: The probability density graph of a continuous random variable is called its distribution curve (figure below). Area of a figure (shaded in the figure) bounded by a curve, straight lines drawn from points a And b perpendicular to the x-axis, and the axis Oh, graphically displays the probability that the value of a continuous random variable X is within the range of a before b. 1. The probability that a random variable will take any value from the interval (and the area of the figure that is limited by the graph of the function f(x) and axis Oh) is equal to one: 2. The probability density function cannot take negative values: and outside the existence of the distribution its value is zero Distribution density f(x), as well as the distribution function F(x), is one of the forms of the distribution law, but unlike the distribution function, it is not universal: the distribution density exists only for continuous random variables. Let us mention the two most important types of distribution of a continuous random variable in practice. If the distribution density function f(x) continuous random variable in some finite interval [ a; b] takes a constant value C, and outside the interval takes a value equal to zero, then this the distribution is called uniform . If the graph of the distribution density function is symmetrical about the center, the average values are concentrated near the center, and moving away from the center those more different from the average are collected (the graph of the function resembles a section of a bell), then this distribution is called normal . Example 1. The probability distribution function of a continuous random variable is known: Find function f(x) probability density of a continuous random variable. Construct graphs of both functions. Find the probability that a continuous random variable will take any value in the interval from 4 to 8: . Solution. We obtain the probability density function by finding the derivative of the probability distribution function: Graph of a function F(x) - parabola: Graph of a function f(x) - straight: Let's find the probability that a continuous random variable will take any value in the range from 4 to 8: Example 2. The probability density function of a continuous random variable is given as: Calculate coefficient C. Find function F(x) probability distribution of a continuous random variable. Construct graphs of both functions. Find the probability that a continuous random variable will take any value in the range from 0 to 5: . Solution. Coefficient C we find, using property 1 of the probability density function: Thus, the probability density function of a continuous random variable is: By integrating, we find the function F(x) probability distributions. If x < 0
, то
F(x) = 0 . If 0< x < 10
, то x> 10, then F(x) = 1
. Thus, the complete record of the probability distribution function is: Graph of a function f(x)
: Graph of a function F(x)
: Let's find the probability that a continuous random variable will take any value in the range from 0 to 5: Example 3. Probability density of a continuous random variable X is given by the equality , and . Find coefficient A, the probability that a continuous random variable X will take any value from the interval ]0, 5[, the distribution function of a continuous random variable X. Solution. By condition we arrive at equality Therefore, , from where . So, Now we find the probability that a continuous random variable X will take any value from the interval ]0, 5[: Now we get the distribution function of this random variable: Example 4. Find the probability density of a continuous random variable X, which takes only non-negative values, and its distribution function  .
. . Find the distribution density of their sum. Find the distribution of the sum of independent random variables x and h, where x has a uniform distribution on the interval, and h has an exponential distribution with parameter l. Find P
. Find the distribution density of their sum. Find the distribution of the sum of independent random variables x and h, where x has a uniform distribution on the interval, and h has an exponential distribution with parameter l. Find P ![]() , if x has: a) normal distribution with parameters a and s2; b) exponential distribution with parameter l; c) uniform distribution on the segment [-1;1]. The joint distribution of x, h is squared uniform
, if x has: a) normal distribution with parameters a and s2; b) exponential distribution with parameter l; c) uniform distribution on the segment [-1;1]. The joint distribution of x, h is squared uniform
K = (x, y): |x| +|y|£ 2). Find probability ![]() . Are x and h independent? A pair of random variables x and h are uniformly distributed inside the triangle K=. Calculate the densities x and h. Are these random variables independent? Find the probability. Random variables x and h are independent and uniformly distributed on the segments and [-1,1]. Find the probability. A two-dimensional random variable (x, h) is uniformly distributed in a square with vertices (2,0), (0,2), (-2, 0), (0,-2). Find the value of the joint distribution function at point (1, -1). A random vector (x, h) is uniformly distributed inside a circle of radius 3 centered at the origin. Write an expression for the joint distribution density. Determine whether these random variables are dependent. Calculate probability. A pair of random variables x and h are uniformly distributed inside a trapezoid with vertices at points (-6,0), (-3,4), (3,4), (6,0). Find the joint distribution density for this pair of random variables and the density of the components. Are x and h dependent? A random pair (x, h) is uniformly distributed inside a semicircle. Find the densities x and h, investigate the question of their dependence. The joint density of two random variables x and h is equal to
. Are x and h independent? A pair of random variables x and h are uniformly distributed inside the triangle K=. Calculate the densities x and h. Are these random variables independent? Find the probability. Random variables x and h are independent and uniformly distributed on the segments and [-1,1]. Find the probability. A two-dimensional random variable (x, h) is uniformly distributed in a square with vertices (2,0), (0,2), (-2, 0), (0,-2). Find the value of the joint distribution function at point (1, -1). A random vector (x, h) is uniformly distributed inside a circle of radius 3 centered at the origin. Write an expression for the joint distribution density. Determine whether these random variables are dependent. Calculate probability. A pair of random variables x and h are uniformly distributed inside a trapezoid with vertices at points (-6,0), (-3,4), (3,4), (6,0). Find the joint distribution density for this pair of random variables and the density of the components. Are x and h dependent? A random pair (x, h) is uniformly distributed inside a semicircle. Find the densities x and h, investigate the question of their dependence. The joint density of two random variables x and h is equal to  .
.
Find the densities x, h. Investigate the question of the dependence of x and h. A random pair (x, h) is uniformly distributed on the set. Find the densities x and h, investigate the question of their dependence. Find M(xh). Random variables x and h are independent and distributed according to the exponential law with the parameter Find![]() .
.![]() And
And![]() , and when
, and when ![]() (Fig. 5).
(Fig. 5).
0,2
0,5
0,3









![]() .
.
![]()


Distribution function of a continuous random variable and probability density
![]() .
.
![]()
![]() .
.![]() .
.
Properties of the probability density function of a continuous random variable
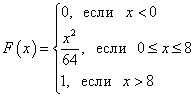



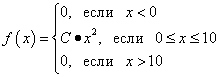


![]() .
.



![]() .
.
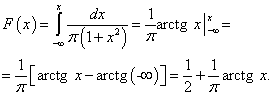
![]() .
.












