How to multiply decimal fractions in a line. Video Tutorial "Multiplication of decimal fractions
In this lesson, we will look at each of these operations separately.
Design of lessonAddition of decimal fractions
As we know, the decimal fraction has a whole and fractional part. When adding decimal fractions, integers and fractional parts are detached separately.
For example, lay decimal fractions 3.2 and 5.3. Decimals more conveniently folded in a column.
We prepare first these two fractions in the column, while the whole parts must be under whole, and fractional under fractional. At school this requirement is called "Comma dressed".
We write the fraction in the column so that the comma is filled:
We begin to add fractional parts: 2 + 3 \u003d 5. We write on the top five in the fractional part of our answer:
Now we fold entire parts: 3 + 5 \u003d 8. Record the eight in the whole part of our answer:
Now separate the semicolons the whole part of the fractional. To do this, again, we observe the rule "Comma dressed":
Received an answer 8.5. It means expressions 3,2 + 5,3 equals 8.5
In fact, not everything is so simple, as it seems at first glance. Here, too, there are their underwater stones, which we will talk about.
Discharges in decimal fractions
In decimal fractions, as in ordinary numbers, there are their discharges. These are discharges of the tenths, the discharge of hundredths, the discharges of thousands. At the same time, the discharge begins after the comma.
The first digit after the comma is responsible for the discharge of the tenths, the second digit after the comma for the discharge of hundredths, the third digit after the comma for the discharge of thousands.
Discharges in decimal fractions keep some useful information. In particular, they report how much in decimal fractions of the tenths, hundredths and thousands of units.
For example, consider the decimal fraction 0,345
The position where the triple is called discharge of tenths
The position where the four is called discharge of hundredths
Position where the fide is called the discharge of thousands

Let's look at this picture. We see that in the discharge of the tenths there is a triple. This suggests that in the decimal fraction 0.345 contains three tenths.
If we fold the fractions, and then we get the original decimal fraction 0,345

It can be seen that at first we got the answer, but transferred it to the decimal fraction and got 0.345.
In addition, decimal fractions are complied with the same principles and rules as when the usual numbers are addition. The addition of decimal fractions occurs in discharges: the tenths are folded with tenth parts, hundredths with hundredths, thousandths with thousands.
Therefore, when adding decimal fractions, you need to comply with the rule "Comma dressed". The comma dive ensures that the very order in which the tenths add up with tits, hundredths with hundredths, thousands of thousands.
Example 1. Find the value of expression 1.5 + 3.4
First of all, we fold fractional parts 5 + 4 \u003d 9. We write down the nine in the fractional part of our answer:
Now we fold entire parts 1 + 3 \u003d 4. Record the fourth in the whole part of our answer:
Now separate the semicolons the whole part of the fractional. To do this, again, we comply with the "comma dive" rule:
Received an answer 4.9. So the value of the expression is 1.5 + 3.4 is 4.9
Example 2. Find an expression value: 3.51 + 1.22
We write in the column This expression, following the "comma dive" rule
First of all, we fold the fractional part, namely the hundredths of the 1 + 2 \u003d 3. We write down the top three in the hundredth of our answer:
Now we fold the tenths of 5 + 2 \u003d 7. We write a seven in the tenth of our answer:
Now we fold entire parts 3 + 1 \u003d 4. We write down the fourth in the whole part of our answer:
Separate the semicolons, the whole part of the fractional, observing the "comma-filled" rule:
Received the answer 4.73. So the value of expression 3.51 + 1,22 is 4.73
3,51 + 1,22 = 4,73
As in conventional numbers, with the addition of decimal fractions can occur. In this case, one digit is written in response, and the rest are transferred to the next discharge.
Example 3. Find an expression value 2.65 + 3,27
We write in the column This expression:
We fold the cells 5 + 7 \u003d 12. The number 12 does not fit in a hundredth of our response. Therefore, in the cell of the part, we write the number 2, and the unit is transferred to the next discharge:
Now we fold the tenths of 6 + 2 \u003d 8 plus a unit that got from the previous operation, we get 9. Record number 9 in the tenth of our answer:
Now we fold entire parts 2 + 3 \u003d 5. Record 5 in the whole part of our answer:
Received 5.92. So the value of the expression 2.65 + 3,27 is 5.92
2,65 + 3,27 = 5,92
Example 4. Find an expression value 9.5 + 2.8
We write in the column this expression
We fold fractional parts 5 + 8 \u003d 13. The number 13 does not fit in the fractional part of our answer, so first write the number 3, and the unit is transferred to the next discharge, more precisely carry it to the integer part:
Now we fold entire parts 9 + 2 \u003d 11 plus a unit that got from the previous operation, we get 12. Record number 12 in the whole part of our answer:
Separate the semicolons the whole part of fractional:
Received 12.3. Means the value of expression 9.5 + 2.8 is 12.3
9,5 + 2,8 = 12,3
When decaying decimal fractions, the number of digits after the comma in both fractions should be the same. If the numbers are missing, then these places in the fractional part are filled with zeros.
Example 5.. Find an expression value: 12,725 + 1.7
Before recording this expression in the column, we will make the number of numbers after the comma in both fractions the same. In the decimal fraction 12.725 after the semicolons, three digits, and in the fraction 1.7 only one. So in the fraction 1.7 at the end you need to add two zero. Then we get a fraction of 1,700. Now you can write this expression in the column and start computing:

We fold the thousands of parts 5 + 0 \u003d 5. Write the figure 5 in the thousandth part of our answer:

We fold the cellular parts 2 + 0 \u003d 2. Write on the number 2 in the hundredth of our answer:

We fold the tenths 7 + 7 \u003d 14. The number 14 does not fit in the tenth of our response. Therefore, first write the number 4, and the unit is transferred to the next discharge:

Now we fold entire parts 12 + 1 \u003d 13 plus a unit that got from the previous operation, we obtain 14. Record number 14 in the whole part of our answer:

Separate the semicolons the whole part of fractional:

Received the answer 14,425. So the value of expression 12,725 + 1,700 is 14,425
12,725+ 1,700 = 14,425
Subtraction decimal fractions
When subtracting decimal fractions, it is necessary to comply with the same rules as when adding: "comma dilated" and "equal number of numbers after a comma."
Example 1. Find the value of the expression 2.5 - 2.2
We record this expression in the column, following the comma duty rule:
Calculate the fractional part 5-2 \u003d 3. Write on the figure 3 in the tenth of our answer:
Calculate the whole part 2-2 \u003d 0. Record zero in the whole part of our answer:
Separate the semicolons the whole part of fractional:
Received 0.3. So the value of expression 2.5 - 2.2 is 0.3
2,5 − 2,2 = 0,3
Example 2. Find an expression value 7,353 - 3.1
In this expression, a different number of numbers after the comma. In the fraction 7.353 after the semicolons, three digits, and in the fraction 3.1 only one. So in the fraction 3.1 at the end you need to add two zero to make the number of numbers in both fractions the same. Then we get 3,100.
Now you can write this expression in the column and calculate it:

Received 4.253 response. Means the value of expression 7,353 - 3.1 is 4.253
7,353 — 3,1 = 4,253
As in conventional numbers, sometimes they will have to occupy a unit from a neighboring discharge, if the subtraction becomes impossible.
Example 3. Find an expression value 3.46 - 2.39
We subtract the hundredth parts 6-9. From the number 6 not to subtract the number 9. Therefore, you need to take a unit from a neighboring discharge. Having taught the unit in the neighboring discharge number 6 refers to the number 16. Now you can calculate the cells of the cells 16-9 \u003d 7. We write down a seven in a hundredth of our answer:
Now we will deduct the tenths. Since we took in the discharge of the tenths of one unit, then the figure that was located there decreased by one unit. In other words, in the discharge of the tenths no longer digit 4, and the figure 3. I calculate the tenths 3-3 \u003d 0. Write zero in the tenth of our answer:
Now we will deduct the whole parts 3-2 \u003d 1. We write down the unit in the whole part of our answer:
Separate the semicolons the whole part of fractional:
Received the answer 1.07. So the value of expression 3,46-2.39 is 1.07
3,46−2,39=1,07
Example 4.. Find an expression value 3-1.2
In this example, a decimal fraction is deducted from an integer. We write this expression by the column so that the whole part of the decimal fraction 1,23 is at number 3
Now we will make the number of numbers after the comma are the same. For this, after the number 3, we will put a comma and add one zero:
Now we will deduct the tenths: 0-2. From zero not subtract number 2. Therefore, you need to take a unit from a neighboring discharge. Taking a unit in a neighboring discharge, 0 refers to the number 10. Now you can calculate the tenths 10-2 \u003d 8. Write the eight in the tenth of our answer:
Now deduct the whole parts. Previously, the number 3 was located in the whole, but we took it one unit. As a result, it appealed to the number 2. Therefore, from 2, we subtract 1. 2-1 \u003d 1. We write down the unit in the whole part of our answer:
Separate the semicolons the whole part of fractional:
Received an answer 1.8. Means the value of expression 3-1,2 is 1.8
Multiplying decimal fractions
Multiplying decimal fractions is simple and even fascinating. In order to multiply decimal fractions, you need to multiply them as conventional numbers, not paying attention to the commas.
Having received the answer, it is necessary to separate the comma to the whole part of the fractional. To do this, it is necessary to calculate the number of numbers after the comma in both fractions, then in response to count the right of the same number and put a comma.
Example 1. Find the value of the expression 2.5 × 1.5
Move these decimal fractions as ordinary numbers, not paying attention to the commas. In order not to pay attention to commas, it is possible to present that they are generally absent:

We received 375. In this regard, it is necessary to separate the semicolons from the fractional. To do this, it is necessary to calculate the number of digits after the comma in fractions 2.5 and 1.5. In the first fraction after the semicolons, one digit, in the second fraction, too alone. Total two digits.
Returning to the number 375 and begin to move right to left. We need to count two digits to the right and put a comma:

Received the answer 3.75. Means the value of the expression 2.5 × 1.5 is 3.75
2.5 × 1 5 \u003d 3.75
Example 2. Find an expression value 12.85 × 2.7
Alternate these decimal fractions, not paying attention to the commas:

We received 34695. In this regard, it is necessary to separate the comma to the whole part of the fractional. To do this, it is necessary to calculate the number of digits after the comma in the fractions of 12.85 and 2.7. In the fraction 12.85 after the semicolons, two digits, in the fraction 2.7 one digit - total three digits.
Returning to the number 34695 and begin to move right to left. We need to count three digits to the right and put a comma:

Received the answer 34.695. Means the value of expression 12.85 × 2.7 is 34,695
12.85 × 2,7 \u003d 34,695
Multiplication of decimal fraction on the usual number
Sometimes there are situations when you need to multiply a decimal fraction on normal number.
In order to multiply the decimal fraction and the usual number, you need to multiply them, not paying attention to the comma in the decimal fraction. Having received the answer, it is necessary to separate the comma to the whole part of the fractional. To do this, it is necessary to calculate the number of numbers after the comma in the decimal fraction, then in response to refer to the right of the same number and put the comma.
For example, multiply 2.54 to 2
We multiply the decimal fraction 2.54 to the usual number 2, not paying attention to the comma:

They received the number 508. In this regard, it is necessary to separate the semicolons the whole part of the fractional. To do this, it is necessary to calculate the number of numbers after the comma in the fraction 2.54. In the fraction 2.54 after the semicolons two digits.
Returning to the number 508 and begin to move right to left. We need to count two digits to the right and put a comma:

Received 5.08. Means the value of the expression 2.54 × 2 is 5.08
2.54 × 2 \u003d 5.08
Multiplying decimal fractions by 10, 100, 1000
The multiplication of decimal fractions by 10, 100 or 1000 is performed in the same way as the multiplication of decimal fractions into conventional numbers. You need to perform multiplication, not paying attention to the comma in the decimal fraction, then in response to separate the whole part of the fractional, squeezing the right of the same number as the numbers were after the semicolons in the decimal fraction.
For example, multiply 2.88 to 10
Multiply decimal fraction 2.88 by 10, not paying attention to the comma in decimal fraction:

Received 2880. In this regard, it is necessary to separate the comma to the whole part of the fractional. To do this, it is necessary to calculate the number of numbers after the semicolon in the fraction 2.88. We see that in the fraction 2.88 after the semicolons two digits.
Returning to the number 2880 and begin to move right to left. We need to count two digits to the right and put a comma:

Received the answer 28.80. We will throw the last zero - we get 28.8. Means the value of the expression 2.88 × 10 is 28.8
2.88 × 10 \u003d 28.8
There is a second way of multiplying decimal fractions by 10, 100, 1000. This method is much easier and more convenient. It lies in the fact that the comma in the decimal fraction moves to the right to so many numbers as zeros in the multiplier.
For example, we solve the previous example of 2.88 × 10 in this way. Do not lead to any calculations, we immediately look at the multiplier 10. We are interested in how much zeros in it. We see that in it one zero. Now in the fraction 2,88 move the comma to the right to one digit, we get 28.8.
2.88 × 10 \u003d 28.8
Let's try to multiply 2.88 per 100. We immediately look at the multiplier 100. We are interested in how much zeros in it. We see that in it two zero. Now in the twist 2,88 move the comma to the right into two digits, we get 288
2.88 × 100 \u003d 288
Let's try to multiply 2.88 per 1000. We immediately look at the factor of 1000. We are interested in how much zeros in it. We see that in it three zero. Now in the twist 2,88 move the comma to the right to three digits. There are no third digits there, so we finish another zero. As a result, we get 2880.
2.88 × 1000 \u003d 2880
Multiplying decimal fractions by 0.1 0.01 and 0.001
The multiplication of decimal fractions by 0.1, 0.01 and 0.001 occurs in the same way as the multiplication of the decimal fraction for a decimal fraction. It is necessary to multiply the fractions as conventional numbers, and in response to put a comma, counting so much the numbers on the right, how many digits after a comma in both fractions.
For example, multiply 3.25 to 0.1
We multiply these fractions, as ordinary numbers, not paying attention to the commas:

Received 325. In this regard, it is necessary to separate the semicolons from the fractional. To do this, it is necessary to calculate the number of numbers after the comma in the frauds 3.25 and 0.1. In the fraction 3.25 after the semicolons, two digits, in the fraction 0.1 one digit. Total three numbers.
We return to the number 325 and begin to move right to left. We need to count three digits to the right and put a comma. After counting the three digits, we discover that the numbers are over. In this case, you need to add one zero and put a comma:

Received 0.325. So the value of expression is 3.25 × 0.1 is 0.325
3.25 × 0.1 \u003d 0.325
There is a second method of multiplication of decimal fractions by 0.1, 0.01 and 0.001. This method is much easier and more convenient. It lies in the fact that the comma in decimal fraction moves to the left of so many numbers as zeros in the multiplier.
For example, we solve the previous example of 3.25 × 0.1 in this way. Do not lead to any calculations immediately look at the multiplier of 0.1. We are interested in how much zeros in it. We see that in it one zero. Now in the fraction 3,25 move the comma left to one digit. After moving the comma on one digit to the left, we see that there are no more numbers before the triple. In this case, add one zero and put the comma. As a result, we get 0.325
3.25 × 0.1 \u003d 0.325
Let's try to multiply 3.25 by 0.01. We immediately look at the multiplier of 0.01. We are interested in how much zeros in it. We see that in it two zero. Now in the fraction 3,25 move the comma to the left into two digits, we get 0.0325
3.25 × 0,01 \u003d 0,0325
Let's try to multiply 3.25 by 0.001. We immediately look at the multiplier of 0.001. We are interested in how much zeros in it. We see that in it three zero. Now in the fraction 3,25 move the comma to the left of three digits, we get 0.00325
3.25 × 0.001 \u003d 0.00325
It is impossible to confuse the multiplication of decimal fractions by 0.1, 0.001 and 0.001 with multiplication by 10, 100, 1000. Typical error Most people.
When multiplying 10, 100, 1000, the comma is transferred to the right to the same number how many zeros in the multiplier.
And with multiplication by 0.1, 0.01 and 0.001, the comma is transferred to the left for the same number how many zeros in the multiplier.
If at first it is difficult to remember, you can use the first method in which multiplication is performed as with conventional numbers. In response, it will be necessary to separate the whole part of the fractional, counting the right of the same number as numbers after the comma in both fractions.
Dividing a smaller number to more. Advanced level.
In one of the previous lessons, we said that when dividing a smaller number, the fraction was greater, in the numerator of which is divisible, and in the denominator - a divider.
For example, to divide one apple for two, you need to write 1 in the numerator (one apple), and write 2 in the denominator (two friends). As a result, we will get a fraction. So each friend will get on the apple. In other words, half of the apple. Fraction is the answer to the task "How to divide one apple for two"

It turns out that it is possible to solve this problem and further if divided 1 at 2. After all, a fractional feature in any fraction means division, which means that this division is allowed. But how? We are accustomed to the fact that Delimi is always more divisor. And here, on the contrary, a divided less divider.
Everything will become clear if you remember that the fraction means crushing, division, separation. And therefore, the unit can be fragmented as many parts, and not only into two parts.
When dividing a smaller number, a decimal fraction is greater, in which the whole part will be 0 (zero). The fractional part can be any.
So, we divide 1 to 2. I will solve this example:
The unit is simply not divided into two units. If you ask a question "How many twists in unity" , then the answer will be 0. Therefore, in private, write 0 and put the comma:
Now, as usual, we multiply the private on the divider to pull out the residue:
The moment came when the unit can be crushed into two parts. To do this, to the right of the received units add another zero:
Received 10. We divide 10 to 2, we get 5. Write on the top five in the fractional part of our answer:
Now pull out the last residue to complete the calculation. Multiply 5 to 2, we get 10
Received 0.5. So the fraction is equal to 0.5
Half of the apple can be recorded and with a decimal fraction 0.5. If you fold these two halves (0.5 and 0.5), we again get the original one-piece apple: 

This moment can also be understood if you represent how 1 cm is divided into two parts. If 1 centimeter is divided into 2 parts, then it turns out 0.5 cm

Example 2. Find an expression value 4: 5
How many tops in the fourth? Not at all. We write in private 0 and put the comma:
We multiply 0 to 5, we get 0. Record zero under the fourth. Immediately deduct this zero from the divide:
Now let's start crushing (divide) the fourth on 5 parts. To do this, to the right of 4 add zero and divide 40 to 5, we get 8. Write the eight in private.

Complete an example, multiplying 8 to 5, and receiving 40:

Received 0.8. So the value of expression 4: 5 is 0.8
Example 3. Find an expression value 5: 125
How many numbers 125 in the five? Not at all. We write 0 in private and put a comma:

We multiply 0 to 5, we get 0. Write 0 under the top five. Immediately subtract 0 from the top five

Now let's start crushing (divide) the top five5 parts. To do this, to the right of this five watering zero:

Delim 50 to 125. How many numbers 125 are among 50? Not at all. So in private again write 0

Multiply 0 to 125, we get 0. We write this zero under 50. Immediately deduct 0 out of 50
Now we divide the number 50 to 125 parts. To do this, to the right of 50, we write another zero:
We divide 500 to 125. How many numbers 125 are among 500. Among the 500 four numbers 125. Write the fourth in private:

Complete an example, multiplying 4 to 125, and receiving 500

Received 0.04. So the value of expression 5: 125 is 0.04
Division of numbers without residue
So, we put a comma in private after the unit, thereby pointing out that the division of integral parts is over and we proceed to the fractional part:
I add zero to the residue 4
Now we divide 40 to 5, we get 8. Record eight in private:
40-40 \u003d 0. Received 0 in the remainder. So division is fully completed. When dividing 9 on 5, a decimal fraction is obtained 1.8:
9: 5 = 1,8
Example 2.. Split 84 by 5 without a residue
At first we divide 84 to 5 as usual with the residue:

Received in private 16 and another 4 in the remainder. Now we divide this residue by 5. We put in a private comma, and I add 4 to the residue 4

Now we divide 40 to 5, we get 8. We write to the eight in the private after the comma:

and complete the example, checking whether there is still the residue:

Decimal decimal fraction on the usual number
Decimal fraction, as we know consists of a whole and fractional part. When dividing decimal fractions to the usual number, first of all, it is necessary:
- split the whole part of the decimal fraction on this number;
- after the whole part is divided, you need to immediately put a comma in a private immediately and continue the calculation as in the usual division.
For example, we divide 4.8 to 2
We write this example to the corner:

Now we divide the whole part on 2. Four divided into two will be two. We write down the two in private and immediately put the comma:
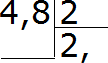
Now I multiply the private on the divider and see whether there is a belt from division:

4-4 \u003d 0. The residue is zero. Zero not yet written, because the solution is not completed. Next, continue to calculate as in the usual division. Demolish 8 and divide it on 2

8: 2 \u003d 4. Record the fourth in private and immediately multiply it on the divider:

Received a response 2.4. The value of 4.8: 2 expression is 2.4
Example 2. Find an expression value 8,43: 3

We divide 8 to 3, we get 2. Immediately put the comma after twos:

Now I multiply the private on the divider of 2 × 3 \u003d 6. We write a six-eight seventh and find the residue:

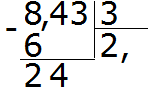
We divide 24 to 3, we get 8. Record the eight in private. Immediately multiply it on the divider to find the balance of division:

24-24 \u003d 0. The residue is zero. Zero not yet written. We demolish the last three of the divide and divide to 3, we get 1. Immediately multiply 1 to 3 to complete this example:

Received the answer 2.81. Means the value of expression 8.43: 3 is 2.81
Decimal decimal fraction for decimal fraction
To divide the decimal fraction to the decimal fraction, it is necessary to transfer comma to the right to the same number in a divider, and then they are after the comma in the divider, and then make division to the usual number.
For example, we divide 5.95 by 1.7
We write this expression

Now in divide and in the divider, we will move the comma to the right to the same number as they are after the comma in the divider. In the divider after a comma one digit. So we must in divide and in the divider move the comma to the right to one digit. Transfer:

After transferring the comma to the right to one digit, the decimal fraction 5,95 turned into a shot 59.5. And the decimal fraction 1.7 after the transfer of the comma to the right to one digit appealed to the usual number 17. And how to share the decimal fraction to the usual number we already know. Further computation is not much difficult:

The comma is transferred to the right to facilitate division. This is allowed due to the fact that when multiplying or dividing the divide and divider on the same number, the private does not change. What does it mean?
This is one of interesting features division. It is called the property of private. Consider the expression 9: 3 \u003d 3. If in this expression, the divider and divider multiply or divided into one and the same number, then the private 3 will not change.
Let's multiply divide and divider for 2, and let's see what happens from this:
(9 × 2): (3 × 2) \u003d 18: 6 \u003d 3
As can be seen from the example, the private has not changed.
The same thing happens when we transfer the comma in Delim and in the divider. In the previous example, where we divided 5.91 by 1.7, we were transferred in divide and divider to the comma on one digit to the right. After the transfer of the comma, the shot 5.91 was transformed into a fraction 59.1 and the fraction 1.7 was transformed into a normal number 17.
In fact, in this process, multiplication took place at 10. That's how it looked:
5.91 × 10 \u003d 59.1
Therefore, on the number of numbers after the comma in the divider, it depends on what the divider and divider will be multiplied. In other words, on the number of numbers after a comma in the divider, it will depend on how many numbers in the division and in the comma divider will be transferred to the right.
Decimal decimal fraction 10, 100, 1000
The division of decimal fractions on 10, 100, or 1000 is carried out in the same way as. For example, we split 2.1 to 10. I will solve this example:

But there is a second way. He is more easy. The essence of this method is that the comma in division is transferred to the left of so many numbers as zeros in the divider.
I decide the previous example in this way. 2.1: 10. We look at the divider. We are interested in how much zeros in it. We see that there is one zero. So in Delima 2.1 you need to move the comma to the left per digit. We transfer the comma to the left to one digit and see that there are no more numbers left. In this case, in front of the digit, add another zero. In the end we get 0.21
Let's try to divide 2.1 per 100. Among the 100 two zero. So in Delim 2.1 it is necessary to transfer the comma to the left into two digits:
2,1: 100 = 0,021
Let us try to divide 2.1 per 1000. Among 1000 three zero. So in Delima 2.1 it is necessary to transfer the comma to the left of three digits:
2,1: 1000 = 0,0021
Decision decimal fraction 0.1, 0,01 and 0.001
Decision decimal fraction 0.1, 0.01, and 0.001 is carried out in the same way as. In Delim and in the divider, you need to transfer the comma to the right to so many numbers as they are after the comma in the divider.
For example, we divide 6.3 to 0.1. First of all, we will transfer commas in divide and in the divider to the right on the same number as they are after the comma in the divider. In the divider after a comma one digit. So we transfer commas in divide and in the divider to the right to one digit.
After transferring the comma to the right to one digit, the decimal fraction 6.3 turns into a normal number 63, and the decimal fraction 0.1 after transferring the comma to the right to one digit turns into one. And divided 63 to 1 is very simple:
So the value of expression 6.3: 0,1 is 63
But there is a second way. He is more easy. The essence of this method is that the comma in division is transferred to the right to so many numbers as zeros in the divider.
I decide the previous example in this way. 6.3: 0.1. We look at the divider. We are interested in how much zeros in it. We see that there is one zero. So in divide 6.3 you need to transfer the comma to the right to one digit. We carry the comma to the right to one digit and get 63
Let us try to divide 6.3 to 0.01. In the divider 0.01 two zero. So in divide 6.3 it is necessary to transfer the comma to the right into two digits. But in division after the comma, only one digit. In this case, at the end you need to add one more zero. As a result, we get 630
Let's try to divide 6.3 to 0.001. In the divider 0.001 three zero. So in divide 6.3 it is necessary to transfer the comma to the right to three digits:
6,3: 0,001 = 6300
Tasks for self-decisions
Did you like the lesson?
Join our new group VKontakte and start receiving notifications about new lessons
§ 1 Application Decimal multiplication rule
In this lesson, you will get acquainted and learn how to apply the rule of multiplication of decimal fractions and the rule of multiplication of decimal fraction on a discharge unit, such as 0.1, 0.01, etc. In addition, we will look at the properties of multiplication when finding values \u200b\u200bof expressions containing decimal fractions.
We will solve the task:
The speed of the vehicle is 59.8 km / h.
What path will overcome the car for 1.3 hours?
As you know, to find a way, you need to multiply speed for a while, i.e. 59.8 Multiply 1.3.

Let's write a number into a column and start multiplying them without noticing the commas: 8 Multiply to 3, it will be 24, 4 Write 2 in the mind, 3 multiply by 9 this is 27, and even plus 2, we get 29, 9 write, 2 in the mind. Now 3 is multiplied by 5, there will be 15 and even add 2, we get 17.
Go to the second line: 1 Multiply 8, it will be 8, 1 multiply by 9, we obtain 9, 1 multiply by 5, we get 5, we fold these two lines, we get 4, 9 + 8 equal to 17, 7 Write 1 in the mind, 7 +9 This is 16 Yes, 1, there will be 17, 7 I write 1 in the mind, 1 + 5 Yes, 1 we get 7.
Now let's see how many signs after commas stands in both decimal fractions! In the first fraction one digit after the comma and in the second fraction one digit after the comma, only two signs. So, on the right in the resulting result, you need to count two digits and put a comma, i.e. There will be 77.74. So, when multiplying 59.8 per 1.3 received 77.74. So the answer in the task is 77.74 km.
Thus, to multiply two decimal fractions it is necessary:
First: perform multiplication, not paying attention to the comma
The second: in the resulting product, separated the semicolons as many numbers to the right, how much they are after the comma in both factors together.
If the numbers in the resulting product are less than it is necessary to separate the semicolon, then ahead must be attributed to one or more zeros.
For example: 0.145 multiply by 0.03 In our product, it turns out 435, and the comma should be separated 5 digits to the right, so we attribute 4 more zero in front of the digit, we put the comma and attribute another zero. We get the answer 0.00435.
§ 2 Properties of multiplication of decimal fractions
With multiplication of decimal fractions, all the same properties of multiplication are preserved, which operate for natural numbers. Let's perform several tasks.
Task number 1:
![]()
Decisive this exampleBy applying the distribution property multiplyingly addition.
5.7 (general multiplier) I will result in a bracket, 3.4 plus 0.6 will remain in brackets. The value of this amount is 4, and now 4 must be multiplied by 5.7, we get 22.8.
Task number 2:
![]()
Apply the multiplication variety property.
2.5 First, multiply by 4, we obtain 10 integers, and now you need to multiply by 32.9 and get 329.
In addition, when multiplying decimal fractions, you can see the following:
When multiplying the number to an incorrect decimal fraction, i.e. Large or equal to 1, it increases or does not change, for example:
![]()
When multiplying the number on the right decimal fraction, i.e. Lower 1, it decreases, for example:
![]()
Let's solve an example:
23,45 multiply by 0.1.
We have to multiply 2 345 to 1 and separate the three silent sign on the right, we get 2,345.
![]()
Now let's decide another example: 23,45 divided by 10, we must transfer the comma to the left for one sign, because 1 zero in the discharge unit, we get 2,345.
From these two examples, we can conclude that multiply the decimal fraction by 0.1, 0.01, 0.001, etc. This means divided the number 10, 100, 1000, etc., i.e. It is necessary in the decimal fraction to transfer the comma to the left for so many signs as zeros standing before 1 in the multiplier.
Using the resulting rule, we will find the values \u200b\u200bof the works:
13.45 multiply by 0.01
in front of the number 1 costs 2 zero, so we move the comma to the left for 2 characters, we get 0.1345.
0,02 multiply by 0.001
in front of the number 1 costs 3 zero, it means that we carry the comma on three signs to the left, we get 0.00002.
Thus, in this lesson you learned to multiply decimal fractions. To do this, you just need to perform multiplication, not paying attention to the commas, and in the resulting product, separated the comma to the right of the right on the right, how much they are after the comma in both factor together. In addition, they got acquainted with the rule of multiplication of decimal fractions by 0.1, 0.01, etc., and also considered the properties of multiplication of decimal fractions.
List of references:
- Mathematics grade 5. Vilekin N.Ya., Zhokhov V.I. et al. 31st ed., Ched. - M: 2013.
- Didactic materials in mathematics grade 5. Author - Popov MA - year 2013
- Calculate without errors. Works with self-test in mathematics 5-6 classes. Author - Minaev S.S. - year 2014
- Didactic materials in mathematics grade 5. Authors: Dorofeyev G.V., Kuznetsova L.V. - 2010 year
- Control I. independent work in mathematics grade 5. Authors - Popov MA - year 2012
- Mathematics. Grade 5: studies. For students, general education. Institutions / I. I. Zubareva, A. G. Mordkovich. - 9th ed., Even. - M.: Mnemozina, 2009
As ordinary numbers.
2. We consider the number of decimal places in the 1st decimal fraction and in the 2nd. Their number fold.
3. In the final result, we count on the right to left such a number of numbers as it turned out in paragraph above, and put the comma.
Rules multiplying decimal fractions.
1. Multiply, not paying attention to the comma.
2. In the work, we separate after the comma, such a number of numbers as they are after commas in both multipliers together.
Multiplying the decimal fraction on the natural number, it is necessary:
1. Multiply numbers, not paying attention to the comma;
2. As a result, we put the comma in such a way that it was so many numbers to the right, as in the decimal fraction.
Multiplying decimal fractions by a column.
Consider on the example:
We write down the decimal fractions in the column and multiply them as natural numbers, not paying attention to the commas. Those. 3.11 we consider as 311, and 0.01 as 1.
The result is 311. Next, we consider the number of signs (numbers) after the comma in both fractions. In the 1st decimal fraction 2 sign and 2 s 2. Total number Figures after commas:
2 + 2 = 4
We count on the right to left four signs from the result. In the final result of numbers less than to separate the comma. In this case, it is necessary to first add a lacking number of zeros.
In our case, it does not reach the 1st digit, so we add left 1 zero on the left.

Note:
Multiplying any decimal fraction at 10, 100, 1000, and so on, the comma in decimal fraction is transferred to the right to so many signs as zeros after a unit.
for example:
70,1 . 10 = 701
0,023 . 100 = 2,3
5,6 . 1 000 = 5 600
Note:
For multiplication of decimal fraction 0.1; 0.01; 0.001; And so on, you need to move the comma to the left for so many signs as zeros in front of the unit.
We consider zero whole!
For example:
12 . 0,1 = 1,2
0,05 . 0,1 = 0,005
1,256 . 0,01 = 0,012 56
You already know that A * 10 \u003d a + a + a + a + a + a + a + a + a + a.For example, 0.2 * 10 \u003d 0.2 + 0.2 + 0.2 + 0.2 + 0.2 + 0.2 + 0.2 + 0.2 + 0.2 + 0.2. It is easy to guess that this amount is 2, i.e. 0.2 * 10 \u003d 2.
Similarly, you can make sure that:
5,2 * 10 = 52 ;
0,27 * 10 = 2,7 ;
1,253 * 10 = 12,53 ;
64,95 * 10 = 649,5 .
You probably guessed that with multiplication of decimal fractions on 10, it is necessary in this fraction to move the comma to the right to one digit.
And how to multiply decimal fraction on 100?
We have: A * 100 \u003d A * 10 * 10. Then:
2,375 * 100 = 2,375 * 10 * 10 = 23,75 * 10 = 237,5 .
Arguing similarly, we get that:
3,2 * 100 = 320 ;
28,431 * 100 = 2843,1 ;
0,57964 * 100 = 57,964 .
Multiply fraction 7,1212 by number 1 000.
We have: 7,1212 * 1 000 \u003d 7,1212 * 100 * 10 \u003d 71212 * 10 \u003d 7121.2.
These examples illustrate the following rule.
To multiply the decimal fraction on 10, 100, 1,000, etc., it is necessary in this fraction to move the comma to the right, respectively, 1, 2, 3, etc., respectively. Numbers.
So, if the comma is transferred to the right on 1, 2, 3, etc. Figures, the fraction will increase accordingly at 10, 100, 1,000, etc. time.
Hence, if the comma is transferred to the left at 1, 2, 3, etc. Figures, the fraction will decrease in 10, 100, 1,000, etc., respectively. time .
We show that the decimal form of recruiting recruiting can multiply them, guided by the rule of multiplication of natural numbers.
We find, for example, a product of 3.4 * 1.23. I will increase the first factor 10 times, and the second is 100 times. This means that we have increased the work of 1,000 times.
Consequently, the product of natural numbers 34 and 123 is 1,000 times more than the desired work.
We have: 34 * 123 \u003d 4182. Then, to obtain an answer, the number 4 182 is reduced by 1,000 times. We write: 4 182 \u003d 4 182.0. Carrying the comma among 4 182.0 per three digits to the left, we obtain the number 4,182, which is 1,000 times less than the number 4 182. Therefore, 3,4 * 1.23 \u003d 4,182.
The same result can be obtained by guided by the following rule.
To multiply two decimal fractions, it is necessary:
1) multiply them as natural numbers, not paying attention to the commas;
2) In the resulting product, separated the comma to the right of the right, as they stand after the commas in both multipliers together.
In cases where the product contains less numbers than it is required to separate the semicol, the left before this, the product is added required amount zeros, and then transfer the comma to the left to the desired number of numbers.
For example, 2 * 3 \u003d 6, then 0.2 * 3 \u003d 0.006; 25 * 33 \u003d 825, then 0.025 * 0.33 \u003d 0.00825.
In cases where one of the multipliers is 0.1; 0.01; 0.001, etc., it is convenient to use the following rule.
To multiply the decimal fraction 0.1; 0.01; 0.001, etc., it is necessary in this fraction to move the comma to the left, respectively, 1, 2, 3, etc., respectively. Numbers.
For example, 1.58 * 0.1 \u003d 0.158; 324.7 * 0.01 \u003d 3,247.
Properties of multiplication of natural numbers are performed for fractional numbers:
aB \u003d BA - Multiplication Movement
(AB) C \u003d A (B C) - the combination property of multiplication,
a (B + C) \u003d AB + AC - the distribution property of multiplication relative to addition.
In this article, we will consider such an action as multiplying decimal fractions. Let's start with the wording of general principles, then we show how to multiply one decimal fraction to another and consider the multiplication method by the column. All definitions will be illustrated by examples. Then we will analyze how to correctly multiply decimal fractions on ordinary, as well as on mixed and natural numbers (including 100, 10, etc.)
As part of this material we will touch only the rules of multiplying positive fractions. Cases with negative disassemble separately in articles on multiplication of rational and valid numbers.
We formulate general principles that must be adhere to when solving problems for multiplying decimal fractions.
Recall to start that decimal fractions are nothing but special form Records of ordinary fractions, therefore, the process of their multiplication can be reduced to similar for the fractions of ordinary. This rule also works for the ultimate, and for endless fractions: after their transfer to ordinary with them it is easy to perform multiplication of the rules already studied by us.
Let's see how such tasks are solved.
Example 1.
Calculate the work 1, 5 and 0, 75.
Solution: To begin with, replace decimal fractions to ordinary. We know that 0, 75 is 75/100, and 1, 5 is 15 10. We can reduce the fraction and produce the whole part. The resulting result of 125 1000 we will write as 1, 125.
Answer: 1 , 125 .
We can use a column counting method as for natural numbers.
Example 2.
Multiply one periodic fraction 0, (3) to another 2, (36).
To begin with, we present the original fractions to ordinary. We will have:
0 , (3) = 0 , 3 + 0 , 03 + 0 , 003 + 0 , 003 + . . . = 0 , 3 1 - 0 , 1 = 0 , 3 9 = 3 9 = 1 3 2 , (36) = 2 + 0 , 36 + 0 , 0036 + . . . = 2 + 0 , 36 1 - 0 , 01 = 2 + 36 99 = 2 + 4 11 = 2 4 11 = 26 11
Consequently, 0, (3) · 2, (36) \u003d 1 3 · 26 11 \u003d 26 33.
Obtained in the end ordinary fraction You can lead to a decimal form by dividing the numerator to the denominator in the column:
Answer: 0, (3) · 2, (36) \u003d 0, (78).
If we have infinite non-periodic fractions in the condition of the problem, then you need to perform their preliminary rounding (see the article on rounding numbers if you forgot how it is done). After that, it is possible to perform multiplication with already rounded decimal fractions. Let us give an example.
Example 3.
Calculate the work 5, 382 ... and 0, 2.
Decision
In our task, there is an infinite fraction that you need to first round up to the hundredths. It turns out that 5, 382 ... ≈ 5, 38. The second factor is rounded to the hundredths of meaning. Now you can calculate the desired work And write out the answer: 5, 38 · 0, 2 \u003d 538 100 · 2 10 \u003d 1 076 1000 \u003d 1, 076.
Answer: 5, 382 ... · 0, 2 ≈ 1, 076.
The counting method of the column can be applied not only for natural numbers. If we have decimal fractions, we can multiply them in the same way. We bring the rule:
Definition 1.
The multiplication of decimal fractions by the column is performed in 2 steps:
1. We perform multiplication by a column, not paying for commas.
2. We put in the final number of the decimal comma, separating it so much figures on the right side, how much both factors contain decimal signs together. If the result is not enough for this numbers, add the left of the zeros.
We will analyze examples of such calculations in practice.
Example 4.
Multiply decimal fractions 63, 37 and 0, 12 column.
Decision
First of all, you will perform multiplication of numbers by ignoring decimal commas.

Now we need to put a comma for the right place. It will separate four numbers on the right side, since the sum of decimal signs in both multipliers is 4. Drop the zeros do not have to do, because Signs enough:

Answer: 3, 37 · 0, 12 \u003d 7, 6044.
Example 5.
Calculate how much it will be 3, 2601 multiply by 0, 0254.
Decision
We consider without registering commas. We get the following:

We will put a comma separating 8 digits on the right side, because the initial fractions together have 8 signs after the comma. But in our result, only seven digits, and we can not do without extra zeros:

Answer: 3, 2601 · 0, 0254 \u003d 0, 08280654.
How to multiply decimal fraction 0.001, 0.01, 01 ,, etc
Multiplying decimal fractions on such numbers has often, so it is important to be able to do it quickly and accurately. We write special rulewhich we will use with such multiplication:
Definition 2.
If we will multiply the decimal fraction on 0, 1, 0, 01, etc., as a result, it turns out a number similar to the original fraction, the comma is transferred to the left for the desired number of characters. When lacking digits for transfer, you need to add zeros to the left.
So, for multiplication 45, 34 to 0, 1 must be transferred in the original decimal fraction with a comma one sign. We will result in 4, 534.
Example 6.
Multiply 9, 4 to 0, 0001.
Decision
We will have to endure the comma for four signs by the number of zeros in the second multiplier, but the numbers in the first will not be enough for this. We attribute the necessary zeros and we obtain that 9, 4 · 0, 0001 \u003d 0, 00094.
Answer: 0 , 00094 .
For infinite decimal fractions, we use the same rule. So, for example, 0, (18) · 0, 01 \u003d 0, 00 (18) or 94, 938 ... · 0, 1 \u003d 9, 4938 .... and etc.
The process of such multiplication is no different effect of multiplying two decimal fractions. It is convenient to use the multiplication method in the column, if the ultimate decimal fraction is worth in the task condition. At the same time, we must take into account all those rules about which we told in the previous paragraph.
Example 7.
Calculate how much it will be 15 · 2, 27.
Decision
Multiply column source numbers and separable two seaste.

Answer: 15 · 2, 27 \u003d 34, 05.
If we are multiplying a periodic decimal fraction on a natural number, you must first change the decimal fraction on the ordinary one.
Example 8.
Calculate the product 0, (42) and 22.
Let us give a periodic fraction to the form of ordinary.
0 , (42) = 0 , 42 + 0 , 0042 + 0 , 000042 + . . . = 0 , 42 1 - 0 , 01 = 0 , 42 0 , 99 = 42 99 = 14 33
0, 42 · 22 \u003d 14 33 · 22 \u003d 14 · 22 3 \u003d 28 3 \u003d 9 1 3
The final result can be written in the form of a periodic decimal fraction as 9, (3).
Answer: 0, (42) · 22 \u003d 9, (3).
Infinite fractions before counting must be pre-rounded.
Example 9.
Calculate how much 4 · 2, 145 ....
Decision
Rounded to the hundredths of the original infinite decimal fraction. After that, we will come to the multiplication of a natural number and the ultimate decimal fraction:
4 · 2, 145 ... ≈ 4 · 2, 15 \u003d 8, 60.
Answer: 4 · 2, 145 ... ≈ 8, 60.
How to multiply decimal fraction per 1000, 100, 10, etc.
Multiplying decimal fraction 10, 100, etc. It is often found in tasks, so we will analyze this case separately. The main rule of multiplication sounds like this:
Definition 3.
To multiply the decimal fraction per 1000, 100, 10, etc., you need to transfer it to the comma on 3, 2, 1 numbers depending on the multiplier and discard the left of the extra zeros. If the digits for the transfer of the comma are not enough, we add so much zeros, how much we need.
Let's show on the example of how to do it.
Example 10.
Perform multiplication 100 and 0, 0783.
Decision
To do this, we need to move in a decimal fraction with a comma on 2 digits to the right side. We obtain in the end 007, 83 zeros, standing on the left, can be discarded and record the result as 7, 38.
Answer: 0, 0783 · 100 \u003d 7, 83.
Example 11.
Multiply 0, 02 by 10 thousand.
Solution: We will carry the comma for four digits to the right. In the original decimal fraction, we will not be enough for this signs, so you have to add zeros. In this case, it will be enough three 0. As a result, it turned out 0, 02000, we move the comma and get 00200, 0. Ignoring zeros on the left, we can write out the answer as 200.
Answer: 0, 02 · 10 000 \u003d 200.
The rule given by us will work as well as in the case of endless decimal fractions, but here you should be very attentive to the period of the final fraction, as it is easy to make an error.
Example 12.
Calculate the work 5, 32 (672) per 1,000.
Solution: First of all, we will write a periodic fraction like 5, 32672672672 ... so the probability will be mistaken less. After that, we can carry the comma for the desired number of signs (for three). As a result, it turns out 5326, 726726 ... We conclude the period in the brackets and write the answer as 5 326, (726).
Answer: 5, 32 (672) · 1 000 \u003d 5 326, (726).
If in the conditions of the problem there are endless non-periodic fractions, which must be multiplied by ten, a hundred, thousand, etc., do not forget to round them before multiplying.
To multiply this type, you need to submit a decimal fraction in the form of an ordinary and continue to act on the already familiar rules.
Example 13.
Multiply 0, 4 to 3 5 6
Decision
In the beginning we will transfer the decimal fraction in the ordinary. We have: 0, 4 \u003d 4 10 \u003d 2 5.
We received an answer in the form of a mixed number. You can write it as a periodic fraction 1, 5 (3).
Answer: 1 , 5 (3) .
If an infinite non-periodic fraction is involved in the calculation, it is necessary to round it up to some numbers and then multiply.
Example 14.
Calculate the work 3, 5678. . . · 2 3.
Decision
We can imagine the second factor as 2 3 \u003d 0, 6666 .... Next, rounded up to the thousandth discharge of both factor. After that, we need to calculate the product of the two finite decimal fractions 3, 568 and 0, 667. Calculate the column and get the answer:

The final result should be rounded up to thousands of stakes, since it is before that discharge we have rounded the initial numbers. We obtain that 2, 379856 ≈ 2, 380.
Answer: 3, 5678. . . · 2 3 ≈ 2, 380
If you notice a mistake in the text, please select it and press Ctrl + Enter
