В какво отношение са разделени височините на триъгълник? Основни елементи на триъгълник abc
E A → ⋅ B C → + E B → ⋅ C A → + E C → ⋅ A B → = 0 (\displaystyle (\overrightarrow (EA))\cdot (\overrightarrow (BC))+(\overrightarrow (EB))\cdot (\ стрелка надясно (CA))+(\стрелка надясно (EC))\cdot (\стрелка надясно (AB))=0)
(За да се докаже идентичността, трябва да се използват формулите
A B → = E B → − E A → , B C → = E C → − E B → , C A → = E A → − E C → (\displaystyle (\overrightarrow (AB))=(\overrightarrow (EB))-(\overrightarrow (EA )),\,(\overrightarrow (BC))=(\overrightarrow (EC))-(\overrightarrow (EB)),\,(\overrightarrow (CA))=(\overrightarrow (EA))-(\overrightarrow (ЕК)))Точката E трябва да се приеме като пресечна точка на двете височини на триъгълника.)
- Ортоцентъризогонално конюгиран с центъра описана окръжност .
- Ортоцентърлежи на същата права като центроида, центърът описана окръжности центъра на окръжността от девет точки (виж линията на Ойлер).
- Ортоцентъростроъгълен триъгълник е центърът на окръжност, вписана в неговия ортотриъгълник.
- Центърът на триъгълник, описан от ортоцентъра с върхове в средите на страните на дадения триъгълник. Последният триъгълник се нарича допълнителен триъгълник по отношение на първия триъгълник.
- Последното свойство може да се формулира по следния начин: Центърът на окръжност, описана около триъгълник служи ортоцентърдопълнителен триъгълник.
- Точки, симетрични ортоцентъртриъгълник по отношение на страните му лежат върху описаната окръжност.
- Точки, симетрични ортоцентъртриъгълници по отношение на средите на страните също лежат върху описаната окръжност и съвпадат с точки, диаметрално противоположни на съответните върхове.
- Ако ОТНОСНОе център на описаната окръжност ΔABC, тогава O H → = O A → + O B → + O C → (\displaystyle (\overrightarrow (OH))=(\overrightarrow (OA))+(\overrightarrow (OB))+(\overrightarrow (OC))) ,
- Разстоянието от върха на триъгълника до ортоцентъра е два пъти разстоянието от центъра на описаната окръжност до срещуположната страна.
- Всеки сегмент, извлечен от ортоцентървинаги разполовява окръжността на Ойлер, докато се пресече с описаната окръжност. Ортоцентъре центърът на хомотетията на тези два кръга.
- Теорема на Хамилтън. Три линейни сегмента, свързващи ортоцентъра с върховете на остроъгълен триъгълник, го разделят на три триъгълника, имащи същата окръжност на Ойлер (окръжност от девет точки) като оригиналния остроъгълен триъгълник.
- Следствия от теоремата на Хамилтън:
- Три отсечки, свързващи ортоцентъра с върховете на остроъгълен триъгълник, го разделят на три Триъгълник на Хамилтънс равни радиуси на описаните окръжности.
- Радиусите на описаните окръжности на трите Триъгълници на Хамилтънса равни на радиуса на окръжността, описана около оригиналния остроъгълен триъгълник.
- В остър триъгълник ортоцентърът лежи вътре в триъгълника; в тъп - извън триъгълника; в правоъгълна - отгоре прав ъгъл.
Свойства на височината на равнобедрен триъгълник
- Ако в триъгълник две височини са равни, тогава триъгълникът е равнобедрен (теоремата на Щайнер-Лемус), а третата височина е едновременно медианата и ъглополовящата на ъгъла, от който излиза.
- Обратното също е вярно: в равнобедрен триъгълник две височини са равни, а третата височина е едновременно медиана и ъглополовяща.
- В равностранен триъгълник всичките три височини са равни.
Свойства на основите на височините на триъгълник
- Основивисочини образуват така наречения ортотриъгълник, който има свои собствени свойства.
- Окръжността, описана близо до ортотриъгълника, е окръжността на Ойлер. Три среди на страните на триъгълника и три среди на трите сегмента, свързващи ортоцентъра с върховете на триъгълника, също лежат върху тази окръжност.
- Друга формулировка на последното свойство:
- Теорема на Ойлер за окръжност от девет точки. Основитри височинипроизволен триъгълник, средите на трите му страни ( основите на вътрешния симедиани) и средните точки на трите сегмента, свързващи върховете му с ортоцентъра, всички лежат на една и съща окръжност (на кръг от девет точки).
- Теорема. Във всеки триъгълник свързващата отсечка основаниядве височинитриъгълник отрязва триъгълник, подобен на дадения.
- Теорема. В триъгълник свързващата отсечка основаниядве височинитриъгълници от двете страни антипаралелентрето лице, с което няма общи точки. През двата му края, както и през два върха на третата спомената страна, винаги е възможно да се начертае окръжност.
Други свойства на височините на триъгълника
Свойства на минималната височина на триъгълник
Минималната височина на триъгълник има много екстремни свойства. Например:
- Минималната ортогонална проекция на триъгълник върху прави, лежащи в равнината на триъгълника, има дължина, равна на най-малката от неговите височини.
- Минималният прав разрез в равнината, през който може да бъде издърпана негъвкава триъгълна плоча, трябва да има дължина, равна на най-малката от височините на тази плоча.
- При непрекъснато движение на две точки по периметъра на триъгълника една към друга максималното разстояние между тях по време на движението от първата среща до втората не може да бъде по-малко от дължината на най-малката от височините на триъгълника.
- Минималната височина в триъгълник винаги е в рамките на този триъгълник.
Основни съотношения
- h a = b sin γ = c sin β , (\displaystyle h_(a)=b\sin \gamma =c\sin \beta ,)
- h a = 2 S a , (\displaystyle h_(a)=(\frac (2S)(a)),)Където S (\displaystyle S)- площ на триъгълник, a (\displaystyle a)- дължината на страната на триъгълника, върху която се спуска височината.
- h a 2 = 1 2 (b 2 + c 2 − 1 2 (a 2 + (b 2 − c 2) 2 a 2)) (\displaystyle h_(a)^(2)=(\frac (1)(2 ))(b^(2)+c^(2)-(\frac (1)(2))(a^(2)+(\frac ((b^(2)-c^(2))^ (2))(a^(2))))))
- h a = b c 2 R , (\displaystyle h_(a)=(\frac (bc)(2R)),)Където пр.н.е. (\displaystyle пр.н.е.)- продуктът на страните, R − (\displaystyle R-)радиус на описаната окръжност
- h a: h b: h c = 1 a: 1 b: 1 c = b c: a c: a b (\displaystyle h_(a):h_(b):h_(c)=(\frac (1)(a)):( \frac (1)(b)):(\frac (1)(c))=bc:ac:ab)
- 1 h a + 1 h b + 1 h c = 1 r (\displaystyle (\frac (1)(h_(a)))+(\frac (1)(h_(b)))+(\frac (1)(h_ (c)))=(\frac (1)(r))), Където r (\displaystyle r)е радиусът на вписаната окръжност.
- S = 1 (1 h a + 1 h b + 1 h c) ⋅ (1 h a + 1 h b − 1 h c) ⋅ (1 h a + 1 h c − 1 h b) ⋅ (1 h b + 1 h c − 1 h a) (\displaystyle S =(\frac (1)(\sqrt (((\frac (1)(h_(a)))+(\frac (1)(h_(b)))+(\frac (1)(h_(c ))))(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(b)))-(\frac (1)(h_(c))) )(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(c)))-(\frac (1)(h_(b))))(\ cdot )((\frac (1)(h_(b)))+(\frac (1)(h_(c)))-(\frac (1)(h_(a)))))))), Където S (\displaystyle S) - площ на триъгълник.
- a = 2 h a ⋅ (1 h a + 1 h b + 1 h c) ⋅ (1 h a + 1 h b − 1 h c) ⋅ (1 h a + 1 h c − 1 h b) ⋅ (1 h b + 1 h c − 1 h a) (\ displaystyle a=(\frac (2)(h_(a)(\cdot )(\sqrt (((\frac (1)(h_(a)))+(\frac (1)(h_(b))) +(\frac (1)(h_(c))))(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(b)))-(\ frac (1)(h_(c))))(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(c)))-(\frac (1 )(h_(b))))(\cdot )((\frac (1)(h_(b)))+(\frac (1)(h_(c)))-(\frac (1)(h_ (а))))))))), a (\displaystyle a)- страната на триъгълника, на която се пада височината h a (\displaystyle h_(a)).
- Височината на равнобедрен триъгълник, спусната до основата: h c = 1 2 4 a 2 − c 2 , (\displaystyle h_(c)=(\frac (1)(2))(\sqrt (4a^(2)-c^(2))),)
Теорема за височината на правоъгълен триъгълник
Ако височината е правоъгълен триъгълник A B C (\displaystyle ABC)дължина h (\displaystyle h), изтеглен от върха на прав ъгъл, разделя хипотенузата с дължина c (\displaystyle c)на сегменти m (\displaystyle m)И n (\displaystyle n)съответстващи на краката b (\displaystyle b)И a (\displaystyle a), то следните равенства са верни.
Триъгълникът е многоъгълник с три страни или затворен прекъсната линияс три връзки или фигура, образувана от три сегмента, свързващи три точки, които не лежат на една права линия (виж фиг. 1).
Основни елементи на триъгълник abc
Върхове – точки A, B и C;
Партита – отсечки a = BC, b = AC и c = AB, свързващи върховете;
ъгли – α , β, γ, образувани от три двойки страни. Ъглите често се означават по същия начин като върховете, с буквите A, B и C.
Ъгълът, образуван от страните на триъгълника и лежащ във вътрешността му, се нарича вътрешен ъгъл, а прилежащият към него ъгъл е прилежащ ъгъл на триъгълника (2, с. 534).
Височини, медиани, ъглополовящи и средни линии на триъгълник
В допълнение към основните елементи в триъгълника се разглеждат и други сегменти, които имат интересни свойства: височини, медиани, ъглополовящи и средни линии.
Височина
Височини на триъгълникса перпендикулярите, пуснати от върховете на триъгълника към противоположните страни.
За да изградите височина, направете следното:
1) начертайте права линия, съдържаща една от страните на триъгълника (ако височината е изтеглена от върха на остър ъгъл в тъп триъгълник);
2) от връх, лежащ срещу начертаната линия, начертайте сегмент от точка до тази линия, сключвайки с нея ъгъл от 90 градуса.


Пресечната точка на надморската височина със страната на триъгълника се нарича височина основа (виж фиг. 2).
Свойства на височината на триъгълника
В правоъгълен триъгълник височината, изтеглена от върха на правия ъгъл, го разделя на два триъгълника, подобни на оригиналния триъгълник.
В остроъгълен триъгълник двете му височини отрязват подобни триъгълници от него.
Ако триъгълникът е остроъгълен, тогава всички основи на височините принадлежат на страните на триъгълника, а за тъп триъгълник две височини падат върху продължението на страните.
Три височини в остроъгълен триъгълник се пресичат в една точка и тази точка се нарича ортоцентър триъгълник.
Медиана
медиани(от латински mediana - "среден") - това са сегменти, свързващи върховете на триъгълника със средните точки на противоположните страни (виж фиг. 3).
За да изградите медиана, направете следното:
1) намерете средата на страната;
2) свържете точката, която е средата на страната на триъгълника, с противоположния връх с отсечка.

Свойства на медианата на триъгълника
Медианата разделя триъгълника на два триъгълника с еднаква площ.
Медианите на триъгълник се пресичат в една точка, която разделя всяка от тях в съотношение 2:1, като се брои от върха. Тази точка се нарича център на тежестта триъгълник.
Целият триъгълник е разделен от своите медиани на шест равни триъгълника.
Симетрала
ъглополовящи(от лат. bis - два пъти "и seko - режа) наричаме сегментите от прави линии, затворени вътре в триъгълника, които разполовяват ъглите му (виж фиг. 4).
За да построите ъглополовяща, трябва да изпълните следните стъпки:
1) конструирайте лъч, излизащ от върха на ъгъла и разделящ го на две равни части (ъглополовяща);
2) намерете пресечната точка на ъглополовящата на ъгъла на триъгълника с противоположната страна;
3) изберете сегмент, свързващ върха на триъгълника с пресечната точка от противоположната страна.
Свойства на ъглополовящата триъгълник
Ъглополовящата на триъгълник разделя противоположната страна по отношение, равно на съотношениетодве съседни страни.
Симетралите на вътрешните ъгли на триъгълник се пресичат в една точка. Тази точка се нарича център на вписаната окръжност.
Симетралите на вътрешния и външния ъгъл са перпендикулярни.
Ако ъглополовящата на външния ъгъл на триъгълника пресича продължението на срещуположната страна, тогава ADBD=ACBC.
Симетралите на един вътрешен и два външни ъгъла на триъгълник се пресичат в една точка. Тази точка е центърът на една от трите вписани окръжности на този триъгълник.
Основите на ъглополовящите на два вътрешни и един външен ъгъл на триъгълник лежат на една права, ако ъглополовящата на външния ъгъл не е успоредна на срещуположната страна на триъгълника.
Ако ъглополовящите на външните ъгли на триъгълник не са успоредни на противоположните страни, тогава техните основи лежат на една права.
Имоти
- Височините на триъгълник се пресичат в една точка, наречена ортоцентър. - Това твърдение е лесно да се докаже с помощта на векторната идентичност, която е валидна за всякакви точки A, B, C, E, не непременно дори лежащи в една и съща равнина:
(За да се докаже идентичността, трябва да се използват формулите
Точката E трябва да се приеме като пресечна точка на двете височини на триъгълника.)
- В правоъгълен триъгълник височината, изтеглена от върха на правия ъгъл, го разделя на два триъгълника, подобни на оригиналния.
- В остроъгълен триъгълник двете му височини отрязват подобни триъгълници от него.
- Основите на височините образуват така наречения ортотриъгълник, който има свои собствени свойства.
Минималната височина на триъгълник има много екстремни свойства. Например:
- Минималната ортогонална проекция на триъгълник върху прави, лежащи в равнината на триъгълника, има дължина, равна на най-малката от неговите височини.
- Минималният прав разрез в равнината, през който може да бъде издърпана негъвкава триъгълна плоча, трябва да има дължина, равна на най-малката от височините на тази плоча.
- При непрекъснато движение на две точки по периметъра на триъгълника една към друга максималното разстояние между тях по време на движението от първата среща до втората не може да бъде по-малко от дължината на най-малката от височините на триъгълника.
Минималната височина в триъгълник винаги е в рамките на този триъгълник.
Основни съотношения
където е площта на триъгълника, е дължината на страната на триъгълника, върху която се спуска височината.
къде е базата.
Теорема за височината на правоъгълен триъгълник
Ако височината на дължина h, изтеглена от върха на правия ъгъл, разделя хипотенузата с дължина c на сегменти m и n, съответстващи на b и a, тогава са верни следните равенства:
Мнемонична поема
Височината е като котка, която, извивайки гърба си под прав ъгъл, свързва върха и страната с опашката си.Вижте също
Връзки
Фондация Уикимедия. 2010 г.
Вижте какво е "Височината на триъгълник" в други речници:
ВИСОЧИНА, височини, мн. височини, височини, женски 1. само единици Разтягане отдолу нагоре, вис. Височина на къщата. Кула с голяма височина. || (мн. само специални научни). Разстояние от земната повърхностизмерено по вертикална линия отдолу нагоре. Самолетът летеше... РечникУшаков
Този термин има и други значения, вижте Височина (многозначност). Височина в елементарна геометриясегмент от перпендикуляр, пуснат от връх геометрична фигура(например триъгълник, пирамида, конус) върху основата му или върху ... ... Wikipedia
височина- с/; мн. високо / ти; и. Вижте също небостъргач, висок 1) Размерът, дължината на какво l. отдолу нагоре, отдолу нагоре. Височина / къщи, дървета, планини. Височина / вълни. Язовир висок сто и петдесет ... Речник на много изрази
с; мн. височина; и. 1. Стойността, дължината на каквото l. отдолу нагоре, отдолу нагоре. V. къщи, дървета, планини. V. вълни. Язовирът е висок сто и петдесет метра. За измерване, определяне на височината на нещо. 2. Разстояние от какво l. повърхност до... енциклопедичен речник
височина на началния триъгълник на резбата- (H) Разстояние между върха и основата на оригиналния триъгълник на резбата в посока, перпендикулярна на оста на резбата. [GOST 11708 82 (ST SEV 2631 80)] Теми на нормата за взаимозаменяемост Обобщаващи термини основните елементи и параметри на нишката EN ... ... Наръчник за технически преводач
Височината е размерът или разстоянието във вертикална посока. Други значения: В астрономията: Височината на светилото е ъгълът между равнината на математическия хоризонт и посоката към светилото. Във военното дело: Височината на котата на релефа. В ... ... Уикипедия
ВИСОЧИНА, в геометрията, отсечка от перпендикуляр, спуснат от върха на геометрична фигура (напр. триъгълник, пирамида, конус) до нейната основа (или продължение на основата), както и дължината на тази отсечка. Височината на призмата, цилиндъра, сферичния слой и ... ... енциклопедичен речник
В геометрията сегмент от перпендикуляр, спуснат от върха на геометрична фигура (напр. триъгълник, пирамида, конус) до нейната основа (или продължение на основата), както и дължината на този сегмент. Височината на призмата, цилиндъра, сферичния слой, както и ... ... Голям енциклопедичен речник
ВИСОЧИНА, s, pl. oty, от, otam, съпруги. 1. Стойността, дължината на която n. отдолу нагоре. V. тухлена зидария. V. прибой. V. циклон. 2. Пространство, разстоянието от земята нагоре. Погледни нагоре. Самолетът набира височина. Лети на...... Обяснителен речник на Ожегов
Височина в геометрията, сегмент от перпендикуляр, спуснат от върха на геометрична фигура (например триъгълник, пирамида, конус) до нейната основа или продължение на основата, както и дължината на този сегмент. V. призма, цилиндър, сферичен слой, ... ... Велика съветска енциклопедия
При решаване на геометрични задачи е полезно да следвате този алгоритъм. Докато четете формулировката на задачата, е необходимо
- Направете рисунка. Чертежът трябва да съответства колкото е възможно повече на условието на проблема, така че основната му задача е да помогне да се намери решението
- Приложете всички данни от условието на задачата към чертежа
- Запишете всички геометрични понятия, които се срещат в проблема
- Припомнете си всички теореми, свързани с тази концепция
- Поставете върху чертежа всички връзки между елементите на геометрична фигура, които следват от тези теореми
Например, ако задачата съдържа думите ъглополовяща на ъгъла на триъгълник, трябва да запомните дефиницията и свойствата на ъглополовящата и да посочите равни или пропорционални сегменти и ъгли на чертежа.
В тази статия ще намерите основните свойства на триъгълник, които трябва да знаете, за да решавате успешно задачи.
ТРИЪГЪЛНИК.
Площ на триъгълник.
1. ,
тук - произволна страна на триъгълника, - височината, спусната до тази страна.

2.
 ,
,
тук и са произволни страни на триъгълника, е ъгълът между тези страни:

3. Формула на Heron:

Тук - дължините на страните на триъгълника, - полупериметърът на триъгълника,
4. ,
тук - полупериметърът на триъгълника, - радиусът на вписания кръг.

Нека са дължините на допирателните сегменти.

Тогава формулата на Heron може да бъде записана в следния вид:
5.

6. ,
тук - дължините на страните на триъгълника, - радиусът на описаната окръжност.

Ако се вземе точка от страна на триъгълник, която разделя тази страна в съотношение m:n, тогава сегментът, свързващ тази точка с върха на противоположния ъгъл, разделя триъгълника на два триъгълника, чиито площи са свързани като m :н:

Съотношението на площите на подобни триъгълници е равно на квадрата на коефициента на подобие.
Медиана на триъгълник
Това е линеен сегмент, който свързва върха на триъгълника със средата на противоположната страна.

Медиани на триъгълникпресичат се в една точка и споделят пресечната точка в съотношение 2:1, като се брои отгоре.

Пресечна точка на медианите правоъгълен триъгълникразделя медианата на два сегмента, по-малкият от които е равен на радиуса на вписаната окръжност, а по-големият е равен на радиуса на описаната окръжност.
 Радиусът на описаната окръжност е два пъти радиуса на вписаната окръжност: R=2r
Радиусът на описаната окръжност е два пъти радиуса на вписаната окръжност: R=2r
Средна дължинапроизволен триъгълник
 ,
,
тук - медианата, изтеглена към страната - дължините на страните на триъгълника.
Симетрала на триъгълник
Това е сегмент от ъглополовящата на всеки ъгъл на триъгълник, свързващ върха на този ъгъл с противоположната страна.

Симетрала на триъгълникразделя страната на сегменти, пропорционални на съседните страни:

Симетрали на триъгълниксе пресичат в една точка, която е центърът на вписаната окръжност.

Всички точки от ъглополовящата на ъгъла са на еднакво разстояние от страните на ъгъла.

Височина на триъгълника
Това е сегмент от перпендикуляра, спуснат от върха на триъгълника до противоположната страна или неговото продължение. В тъп триъгълник надморската височина, изтеглена от върха на остър ъгъл, е извън триъгълника.

Височините на триъгълник се пресичат в една точка, която се нарича ортоцентъра на триъгълника.
Да се намери височината на триъгълникизтеглен отстрани, трябва да намерите неговата площ по всякакъв възможен начин и след това да използвате формулата:
Център на окръжност, описана около триъгълник, се намира в точката на пресичане на ъглополовящите, начертани към страните на триъгълника.

Радиусът на описаната окръжност на триъгълник може да се намери с помощта на следните формули:
Тук са дължините на страните на триъгълника и е площта на триъгълника.
 ,
,
където е дължината на страната на триъгълника, е срещуположният ъгъл. (Тази формула следва от синусовата теорема).
неравенство на триъгълник
Всяка страна на триъгълника е по-малка от сбора и по-голяма от разликата на другите две.
Сумата от дължините на всеки две страни винаги е по-голяма от дължината на третата страна:
Срещу по-голямата страна лежи по-голям ъгъл; срещу по-големия ъгъл лежи по-голямата страна:
Ако , то обратното.
Синусова теорема:
Страните на триъгълника са пропорционални на синусите на противоположните ъгли:


Косинусова теорема:
квадратна страна на триъгълник е равно на суматаквадрати на другите две страни, без да се удвоява произведението на тези страни по косинуса на ъгъла между тях:
![]()
Правоъгълен триъгълник
- Това е триъгълник с един от ъглите, равен на 90°.
Сума остри ъглиправоъгълният триъгълник е 90°.
Хипотенузата е страната, която лежи срещу ъгъла от 90°. Хипотенузата е най-дългата страна.
Питагорова теорема:
квадратът на хипотенузата е равен на сумата от квадратите на катетите: ![]()

Радиусът на окръжност, вписана в правоъгълен триъгълник, е
 ,
,
тук - радиусът на вписаната окръжност, - краката, - хипотенузата:

Център на окръжност, описана около правоъгълен триъгълник лежи в средата на хипотенузата:
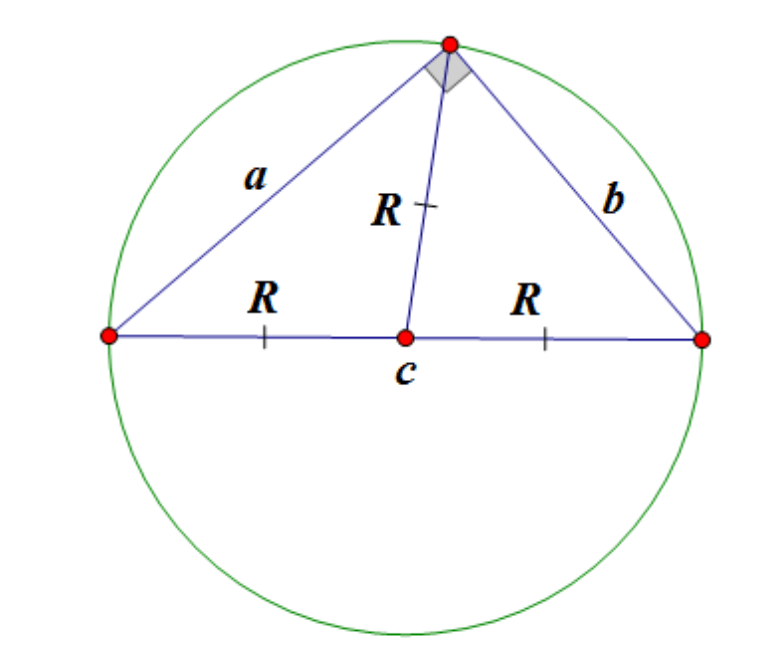
Медиана на правоъгълен триъгълник, начертана към хипотенузатаравно на половината от хипотенузата.
Дефиниция на синус, косинус, тангенс и котангенс на правоъгълен триъгълниквиж
Съотношението на елементите в правоъгълен триъгълник:
Квадратът на височината на правоъгълен триъгълник, изтеглен от върха на правия ъгъл, е равен на произведението на проекциите на краката към хипотенузата:
![]()
Квадратът на катета е равен на произведението на хипотенузата и проекцията на катета към хипотенузата:

Крак, лежащ срещу ъгъла равно на половината от хипотенузата:

![]()
Равнобедрен триъгълник.
Симетралата на равнобедрен триъгълник, начертана към основата, е медиана и височина.
В равнобедрен триъгълник ъглите при основата са равни.

Горен ъгъл.
I - страни
И - ъгли в основата.
Височина, ъглополовяща и медиана.
внимание!Височината, ъглополовящата и медианата, начертани към страничната страна, не съвпадат.
правоъгълен триъгълник
(или равностранен триъгълник ) е триъгълник, всички страни и ъгли на който са равни.

Площ на равностранен триъгълнике равно на
където е дължината на страната на триъгълника.
Център на окръжност, вписана в равностранен триъгълник, съвпада с центъра на окръжността, описана около равностранен триъгълник и лежи в точката на пресичане на медианите.
Пресечна точка на медиани на равностранен триъгълникразделя медианата на два сегмента, по-малкият от които е равен на радиуса на вписаната окръжност, а по-големият е равен на радиуса на описаната окръжност.
Ако един от ъглите на равнобедрен триъгълник е 60°, то триъгълникът е правилен.
Средна линия на триъгълника
Това е сегмент, който свързва средните точки на двете страни.
На фигурата DE е средната линия на триъгълник ABC.
Средната линия на триъгълника е успоредна на третата страна и равна на нейната половина: DE||AC, AC=2DE

Външен ъгъл на триъгълник
Това е ъгълът, съседен на всеки ъгъл на триъгълника.
Външен ъгъл на триъгълник е равен на сбора от два ъгъла, които не са съседни на него.

Тригонометрични функции на външен ъгъл:
Признаци за равенство на триъгълници:
1 . Ако две страни и ъгълът между тях на един триъгълник са съответно равни на две страни и ъгълът между тях на друг триъгълник, тогава тези триъгълници са еднакви.

2 . Ако страна и два съседни ъгъла на един триъгълник са съответно равни на страна и два съседни ъгъла на друг триъгълник, тогава тези триъгълници са еднакви.

3 Ако три страни на един триъгълник са съответно равни на три страни на друг триъгълник, тогава тези триъгълници са еднакви.

Важно:тъй като в правоъгълен триъгълник два ъгъла са очевидно равни, тогава за равенство на два правоъгълни триъгълникасамо два елемента трябва да бъдат равни: две страни или страна и остър ъгъл.
Признаци за сходство на триъгълници:
1 . Ако две страни на един триъгълник са пропорционални на две страни на друг триъгълник и ъглите между тези страни са равни, тогава тези триъгълници са подобни.
2 . Ако три страни на един триъгълник са пропорционални на три страни на друг триъгълник, тогава тези триъгълници са подобни.
3 . Ако два ъгъла на един триъгълник са равни на два ъгъла на друг триъгълник, тогава тези триъгълници са подобни.
Важно: V подобни триъгълнициПодобни страни лежат срещу равни ъгли.
Теорема на Менелай
Нека правата пресича триъгълника, където е точката на нейното пресичане със страната, е точката на нейното пресичане със страната и е точката на нейното пресичане с продължението на страната. Тогава

Теорема за височината на правоъгълен триъгълник
Ако височината в правоъгълен триъгълник ABC с дължина, изведена от върха на правия ъгъл, разделя хипотенузата на дължината на сегменти и съответстващи на краката и , тогава са верни следните равенства:
· ![]()
· ![]()
Свойства на основите на височините на триъгълник
· Основивисочини образуват така наречения ортотриъгълник, който има свои собствени свойства.
· Описаната около ортотриъгълника окръжност е окръжността на Ойлер. Три среди на страните на триъгълника и три среди на трите сегмента, свързващи ортоцентъра с върховете на триъгълника, също лежат върху тази окръжност.
Друга формулировка на последното свойство:
· Теорема на Ойлер за окръжност от девет точки.
Основитри височинипроизволен триъгълник, средите на трите му страни ( основите на вътрешния симедиани) и средните точки на трите сегмента, свързващи върховете му с ортоцентъра, всички лежат на една и съща окръжност (на кръг от девет точки).
· Теорема. Във всеки триъгълник свързващата отсечка основаниядве височинитриъгълник отрязва триъгълник, подобен на дадения.
· Теорема. В триъгълник свързващата отсечка основаниядве височинитриъгълници от двете страни антипаралелентрето лице, с което няма допирни точки. През двата му края, както и през два върха на третата спомената страна, винаги е възможно да се начертае окръжност.
Други свойства на височините на триъгълника
Ако триъгълникът универсален (скален), тогава неговото вътрешниъглополовящата, начертана от всеки връх, лежи между вътрешнимедиана и височина, изтеглени от един и същи връх.
Височината на триъгълник е изогонално свързана с диаметъра (радиуса) описана окръжностизтеглен от същия връх.
Остроъгълният триъгълник има две височиниотрежете подобни триъгълници от него.
В правоъгълен триъгълник височина, изтеглен от върха на прав ъгъл, го разделя на два триъгълника, подобни на първоначалния.
Свойства на минималната височина на триъгълник
Минималната височина на триъгълник има много екстремни свойства. Например:
· Минималната ортогонална проекция на триъгълник върху прави, лежащи в равнината на триъгълника, има дължина, равна на най-малката от неговите височини.
· Минималният прав разрез в равнината, през който може да бъде издърпана негъвкава триъгълна плоча, трябва да има дължина, равна на най-малката от височините на тази плоча.
· При непрекъснато движение на две точки по периметъра на триъгълника една към друга максималното разстояние между тях по време на движението от първата среща до втората не може да бъде по-малко от дължината на най-малката от височините на триъгълника.
· Минималната височина в триъгълник винаги е в рамките на този триъгълник.
Основни съотношения
·  където е площта на триъгълника, е дължината на страната на триъгълника, върху която се спуска височината.
където е площта на триъгълника, е дължината на страната на триъгълника, върху която се спуска височината.
·  където е произведението на страните, радиусът на описаната окръжност
където е произведението на страните, радиусът на описаната окръжност
·  ,
,
където е радиусът на вписаната окръжност.
Къде е площта на триъгълника.
къде е страната на триъгълника, към която се спуска височината.
Височината на равнобедрен триъгълник, спусната до основата:

къде е базата.
·  е височината в равностранен триъгълник.
е височината в равностранен триъгълник.
Медиани и височини в равностранен триъгълник
Медианите на триъгълник се пресичат в една точка, която разделя всяка от тях в съотношение 2:1, като се брои от върха. Тази точка се нарича център на тежесттатриъгълник. А в равностранните триъгълници медианите и височините са едно и също нещо.

Да разгледаме произволен триъгълник ABC. Нека O означава пресечната точка на неговите медиани AA1 и BB1 и начертайте средна линия A1B1 на този триъгълник Медианите на триъгълника се пресичат в една точка.Отсечката A1B1 е успоредна на страната AB, следователно ъгли 1 и 2, както и ъгли 3 и 4 са равни като кръстосани ъгли при пресичане на успоредни прави AB и A1B1 чрез секущите AA1 и BB1. Следователно триъгълниците AOB и A1OB1 са подобни в два ъгъла и следователно техните страни са пропорционални: AOA1O=BOB1O=ABA1B1 . Но AB=2⋅A1B1, така че AO=2⋅A1O и BO=2⋅B1O. Така пресечната точка O на медианите AA1 и BB1 разделя всяка от тях в съотношение 2:1, като се брои отгоре. По същия начин се доказва, че пресечната точка на медианите BB1 и CC1 разделя всяка от тях в съотношение 2:1, считано от върха, и следователно съвпада с точката O. Така че и трите медиани на триъгълника ABC се пресичат в точка O и я разделете в съотношение 2:1, като броите отгоре.
Теоремата е доказана.

Представете си, че във върховете на ъгъла m₁=1, след това в точките A₁, B₁, C₁, m₂=2, тъй като те са средните точки на страните. И тук можете да видите, че сегментите AA₁, BB₁, CC₁, които се пресичат в една точка и изглеждат като лостове с опорна точка O, където AO-l₁ и OA₁-l₂ (рамена). И според физическата формула F₁/F₂=l₁/l₂, където F=m*g, където g-const, и съответно се редуцира, се получава m₁/m₂=l₁/l₂, т.е. ½=1/2.
Теоремата е доказана.
ортотриъгълник
Имоти:
Три височини на триъгълник се пресичат в една точка, тази точка се нарича ортоцентър
две съседни страниформират ортотриъгълници равни ъглисъс съответната страна на оригиналния триъгълник
Височините на триъгълник са ъглополовящи на ортотриъгълник
Ортотриъгълник е триъгълник с най-малък периметър, който може да бъде вписан даден триъгълник(Проблем с Фаняно)
· Периметърът на ортотриъгълника е равен на удвоеното произведение от височината на триъгълника и синуса на ъгъла, от който произлиза.
Ако точките A 1 , B 1 и C 1 съответно от страните BC, AC и AB на остроъгълен триъгълник ABC са такива, че
тогава е ортотриъгълникът на триъгълник ABC.
Ортотриъгълник отрязва триъгълници като дадения.

Теорема за свойството на ъглополовящите на ортотриъгълник

∟ B₁C₁C=∟B₁BC=∟CAA₁=∟CC₁A
CC₁-ъглополовяща ∟B₁C₁A
AA₁-ъглополовяща ∟B₁A₁C₁
BB₁-ъглополовяща ∟A₁B₁C₁
